
已知一抛物线经过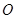 (0,0),
(0,0), (1,1)两点,且解析式的二次项系数为
(1,1)两点,且解析式的二次项系数为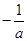
( >0).
>0).
【小题1】当 时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
【小题2】已知点 (0,1),若抛物线与射线
(0,1),若抛物线与射线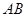 相交于点
相交于点 ,与
,与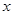 轴相交于点
轴相交于点 (异于原点),当
(异于原点),当 在什么范围内取值时,
在什么范围内取值时,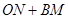 的值为常数?当
的值为常数?当 在什么范围内取值时,
在什么范围内取值时, 的值为常数?
的值为常数?
【小题3】若点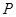 (
(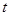 ,
,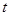 )在抛物线上,则称点
)在抛物线上,则称点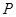 为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线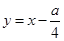 上,请说明理由.
上,请说明理由.
【小题1】设该抛物线的解析式为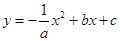 ,
,
∵抛物线经过(0,0)、(1,1)两点,
∴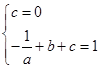 ,解得
,解得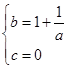 .
.
∴该抛物线的解析式为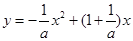 ………………………………………1分
………………………………………1分
(Ⅰ)当 时,该抛物线的解析式为
时,该抛物线的解析式为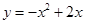 …………………………2分
…………………………2分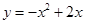
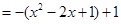
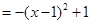 .
.
该抛物线的顶点坐标为(1,1) . ……………………………………3分
【小题2】∵点 在
在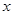 轴上,∴点
轴上,∴点 的纵坐标为0.
的纵坐标为0.
当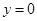 时,有
时,有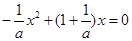 ,解得
,解得 ,
,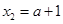 .
.
∵点 异于原点,∴点
异于原点,∴点 的坐标为(
的坐标为(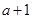 ,0).∴
,0).∴ ………………4分
………………4分
∵点 在射线
在射线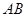 上,∴点
上,∴点 的纵坐标为1.
的纵坐标为1.
当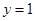 时,有
时,有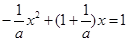 ,
,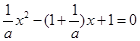 ,
,
解得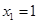 ,
,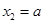 .
.
点 的坐标为(1,1)或(
的坐标为(1,1)或( ,1) . ……………………………5分
,1) . ……………………………5分
当点 的坐标为(1,1)时,
的坐标为(1,1)时, 与
与 重合,此时
重合,此时 ,
,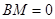 ,
,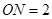 .
.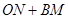 与
与 的值都是常数2.
的值都是常数2.
当点 的坐标为(
的坐标为( ,1)时,
,1)时,
若点 在点
在点 右侧,此时
右侧,此时 >1,
>1,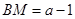 .
.
∴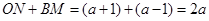 ,
,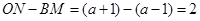 .
.
若点 在点
在点 左侧,此时0<
左侧,此时0< <1,
<1,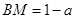 .
.
∴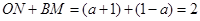 ,
,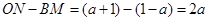 .
.
∴当0< ≤1时,
≤1时,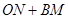 的值是常数2. ..………………………………6分
的值是常数2. ..………………………………6分
当 ≥1时,
≥1时, 的值是常数2. ……………………………………7分
的值是常数2. ……………………………………7分
【小题3】设平移后的抛物线的解析式为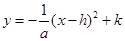 ,
,
由不动点的定义,得方程: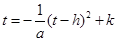 , ………………8分
, ………………8分
即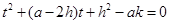 .
.
∵平移后的抛物线只有一个不动点,∴此方程有两个相等的实数根.
∴判别式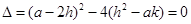 , .…………………9分
, .…………………9分
有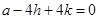 ,
,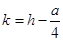 .
.
∴顶点(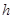 ,
,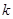 )在直线
)在直线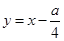 上. …………………………………10分
上. …………………………………10分
解析


科目:初中数学 来源: 题型:
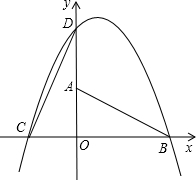 ,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.
,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| a |
| a |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (a>0).
(a>0). 上,请说明理由.
上,请说明理由.查看答案和解析>>
科目:初中数学 来源:2013年湖北省黄石九中中考数学模拟试卷(一)(解析版) 题型:解答题
 (a>0).
(a>0). 上,请说明理由.
上,请说明理由.查看答案和解析>>
科目:初中数学 来源:2012年天津市红桥区中考数学二模试卷(解析版) 题型:解答题
 (a>0).
(a>0). 上,请说明理由.
上,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com