
【题目】如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数.

【答案】(1)45°(2)![]() α(3)45°
α(3)45°
【解析】
(1)要求∠MON,即求∠COM-∠CON,再根据角平分线的概念分别进行计算即可求得;
(2)和(3)均根据(1)的计算方法进行推导即可.
解:(1)∵∠AOB=90°,∠AOC=30°,
∴∠BOC=120°.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=60°,∠CON=15°,
∴∠MON=∠COM-∠CON=45°;
(2)∵∠AOB=α,∠AOC=30°,
∴∠BOC=α+30°.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=![]() α+15°,∠CON=15°,
α+15°,∠CON=15°,
∴∠MON=∠COM-∠CON=![]() α;
α;
(3)∵∠AOB=90°,∠AOC=β,
∴∠BOC=90°+β.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=45°+![]() β,∠CON=
β,∠CON=![]() β,
β,
∴∠MON=∠COM-∠CON=45°.


科目:初中数学 来源: 题型:
【题目】如图,是由一些棱长都为1的小正方体组合成的简单几何体.

(1)请画出这个几何体的三视图并用阴影表示出来;
(2)该几何体的表面积(含下底面)为 ;
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菲尔兹奖是国际上有崇高声誉的一个数学奖项,下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄(岁): 29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
请根据上述数据,解答下列问题:
小彬按“组距为5”列出了如图的频数分布表
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
合计 | 56 |
(1)每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图; 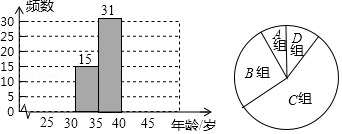
(2)根据(1)中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征;
(3)在(1)的基础上,小彬又画了如图所示的扇形统计图,图中获奖年龄在30~35岁的人数约占获奖总人数的%(百分号前保留1位小数);C组所在扇形对应的圆心角度数约为°(保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“足球进校园”的号召,某学校决定在商场购买甲、乙两种品牌的足球.已知乙种品牌足球比甲种品牌足球每只贵10元,该校欲分别花费2000元、1200元购买甲、乙两种足球,这样购得甲种足球的数量是购得乙种足球的数量的2倍.求甲、乙两种足球的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1= ![]() 的图象与一次函数y2=
的图象与一次函数y2= ![]() x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=
x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1= ![]() 的图象上.
的图象上. 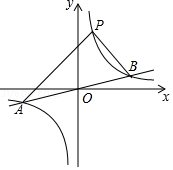
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为-1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上A、B两点所表示的数分别为-2和8.
(1)求线段AB的长;
(2)若P为射线BA上的一点(点P不与A、B两点重合,M为PA的中点,N为PB的中点,当点P在射线BA上运动时;MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com