
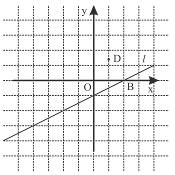
如图,已知直线l的解析式为y = 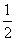 x–1,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D
x–1,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D  三点.
三点.
(1)求抛物线的解析式及A点的坐标,并在图示坐标系中画出抛物线的大致图象;
(2)已知点 P(x,y)为抛物线在第二象限部分上的一个动点,过点P作PE垂直x轴于点E, 延长PE与直线l交于点F,请你将四边形PAFB的面积S表示为点P的横坐标x的函数, 并求出S的最大值及S最大时点P的坐标;
(3)将(2)中S最大时的点P 与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.
与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.
解:(1)∵ y = ax2+bx+2经过点B、D
∴ 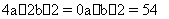
解之得:a =–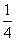 ,b =–
,b =–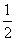
∴ y =–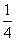 x2 –
x2 –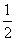 x+2
x+2
∵ A(m,0)在抛物线上
∴ 0 =–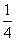 m2 –
m2 –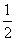 m+2
m+2
解得:m =–4
∴ A(–4,0)
图像(略)
(2)由题设知直线l的解析式为y = 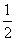 x–1
x–1
∴ S = 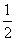 AB·PF
AB·PF
= 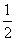 ×6·PF
×6·PF
= 3(–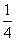 x2 –
x2 –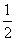 x+2+1–
x+2+1–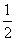 x)
x)
= –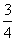 x2 –3x+9
x2 –3x+9
= –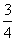 (x+2)2 +12
(x+2)2 +12
其中–4 < x < 0
∴ S最大= 12,此时点P的坐标为(–2,2)
(3)∵ 直线PB过点P(–2,2)和点B(2,0)
∴ PB所在直线的解析式为y =–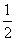 x+1
x+1
设Q(a,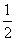 a–1)是
a–1)是 y =
y = 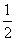 x–1上的任一点
x–1上的任一点
则Q点关于x轴的对称点为(a,1–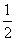 a)
a)
将(a,1–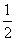 a)代入y =–
a)代入y =–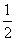 x+1显然成立
x+1显然成立
∴ 直线l上任意一点关于x轴的对称点一定在PB所在的直线上


科目:初中数学 来源: 题型:
从广州某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的 行驶路程的1.3倍.
行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
学校为了了解初三年级学生体育跳绳的训练情况,从初三年级各班随机抽取了50名学生进行了60秒跳绳的测试,并将这50名学生的测试成绩(即60秒跳绳的个数)从低到高分成六段记为第一到六组,最后整理成下面的频数分布直方图:请根据直方图中样本数据提供的信息解答下列问题.
(1)跳绳次数的中位数落在哪一组?由样本数据的中位数你能推断出学 校初三年级学生关于60秒跳绳成绩的一个什么结论?
校初三年级学生关于60秒跳绳成绩的一个什么结论?
(2)若用各组数据的组中值(各小组的两个端点的数的平均数)代表各组的实际数据,求这50名学生的60秒跳绳的平均成绩(结果保留整数);
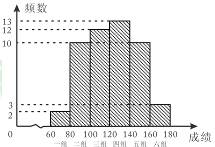 (3)若从成绩落在第一和第六组的学生中随机抽取2名学生,用列举法求抽取的2名学生恰好在
(3)若从成绩落在第一和第六组的学生中随机抽取2名学生,用列举法求抽取的2名学生恰好在 同一组的概率.
同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,把一块含有45°角的直角三角板两个顶点放在直尺的对边上,如果∠1=20°,则∠2的度数是( )
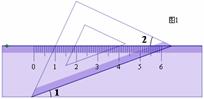 A、15° B、20° C、25° D、30°
A、15° B、20° C、25° D、30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com