Question

如图，点C为线段AB上一点，△ACM，△CBN是等边三角形，直线AN，MC交于点E，直线BM，CN交于点F．

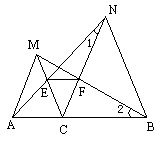
(1)求证：AN＝BM；

(2)求证：△CEF是等边三角形；

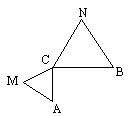
(3)将△ACM绕点C按逆时针方向旋转，其他条件不变．在下图中补出符合要求的图形，并判断第(1)(2)两小题的结论是否仍然成立(不要求证明)．

Answer 1

答案：
解析：

(1)证明：∵△ACM、△CBN是等边三角形． 　　∴AC＝MC，CN＝CB，∠ACM＝∠BCN＝． 　　∴∠ACN＝∠MCB． 　　∴△ACN≌△MCB．∴AN＝BM． 　　(2)证明：由△ACN≌△MCB，得∠1＝∠2， 　　又CN＝CB，∠BCF＝∠NCE＝，∴△BCF≌△NCE． 　　∴CE＝CF． 　　又∠ECF＝，∴△ECF为等边三角形． 　　(3)补出图形如图，AN＝BM仍然成立，△CEF是等边三角形不成立． 　　剖析：此题综合考查了等边三角形的性质和判定，但在求解的过程中，由于图形在旋转，容易忽视∠ECF＝这一结论，在第(3)问中，不能正确补出图形，导致探索结论出现错误．虽然此题在运动中求变化，但在处理问题时，要在运动中求静止，在静止中去思考、去探索．