
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾µÄ”°Ńī»ŌČż½Ē”±øęĖßĮĖĪŅĆĒ¶žĻīŹ½³Ė·½Õ¹æŖŹ½µÄĻµŹż¹ęĀÉ£¬Čē£ŗµŚČżŠŠµÄČżøöŹż£Ø1”¢2”¢1£©Ē”ŗƶŌÓ¦×Å£Øa+b£©2µÄÕ¹æŖŹ½a2+2ab+b2µÄĻµŹż£»µŚĖÄŠŠµÄĖÄøöŹżĒ”ŗƶŌÓ¦×Å£Øa+b£©3£½a3+3a2b+3ab2+b3µÄĻµŹż£¬øł¾ŻŹż±ķÖŠĒ°Ī劊µÄŹż×ÖĖł·“Ó³µÄ¹ęĀÉ£¬»Ų“š£ŗ
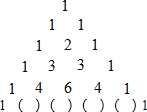
£Ø1£©Ķ¼ÖŠµŚĮłŠŠĄØŗÅĄļµÄŹż×Ö·Ö±šŹĒ”” ””£»£ØĒė°““Ó×óµ½ÓŅµÄĖ³ŠņĢīŠ“£©
£Ø2£©£Øa+b£©4£½”” ””£»
£Ø3£©ĄūÓĆÉĻĆęµÄ¹ęĀɼĘĖćĒóÖµ£ŗ£Ø![]() £©4©4”Į£Ø
£©4©4”Į£Ø![]() £©3+6”Į£Ø
£©3+6”Į£Ø![]() £©2©4”Į
£©2©4”Į![]() +1£®
+1£®
£Ø4£©Čō£Ø2x©1£©2018£½a1x2018+a2x2017+a3x2016+””+a2017x2+a2018x+a2019£¬Ēóa1+a2+a3+””+a2017+a2018µÄÖµ£®
”¾“š°ø”æ(1) 5£¬10£¬10£¬5£»(2) ![]() £»(3)
£»(3) ![]() £»(4)0
£»(4)0
”¾½āĪö”æ
£Ø1£©øł¾Ż”°Ńī»ŌČż½Ē”±¹ęĀÉČ·¶Ø³öµŚĮłŠŠĄØŗÅĄļµÄŹż×Ö¼“æÉ£»
£Ø2£©øł¾Ż”°Ńī»ŌČż½Ē”±ÖŠµÄĻµŹżČ·¶Ø³öŌŹ½Õ¹æŖ½į¹ū¼“æÉ£»
£Ø3£©ŌŹ½ÄęÓĆ”°Ńī»ŌČż½Ē”±ĻµŹż¹ęĀɱäŠĪ£¬¼ĘĖć¼“æɵƵ½½į¹ū£®
£Ø4£©µ±x=0£¬ĻČĒó³ö![]() £¬µ±x=1Ź±£¬“śČėŌŹ½¼ĘĖć£¬¼“æÉĒó³ö“š°ø.
£¬µ±x=1Ź±£¬“śČėŌŹ½¼ĘĖć£¬¼“æÉĒó³ö“š°ø.
½ā£ŗ£Ø1£©øł¾ŻĶ¼ÖŠ¹ęĀÉ£ŗµŚĮłŠŠĄØŗÅĄļµÄŹż×Ö·Ö±šĪŖ£ŗ5£¬10£¬10£¬5£»
£Ø2£©![]() £»
£»
£Ø3£©ŌŹ½£½![]() £»
£»
£Ø4£©µ±x£½0Ź±£¬![]() £¬
£¬
µ±x£½1Ź±£¬![]() £¬
£¬
”ą![]() £»
£»


 ĒįĒɶį¹ŚÖܲāŌĀæ¼Ö±ĶØÖŠæ¼ĻµĮŠ“š°ø
ĒįĒɶį¹ŚÖܲāŌĀæ¼Ö±ĶØÖŠæ¼ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚČń½Ē”÷ABCÖŠ£¬AC£½8£¬”÷ABCµÄĆ껿ĪŖ20£¬”ĻBACµÄĘ½·ÖĻß½»BCÓŚµćD£¬M£¬N·Ö±šŹĒADŗĶABÉĻµÄ¶Æµć£¬ŌņBM£«MNµÄ×īŠ”ÖµŹĒ________.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓÉÓŚÄ³µŲ¹©Ė®¹Ü±¬ĮŃ.øƵŲ¹©Ė®²æĆÅ×éÖƹ¤ČĖ½ųŠŠĒĄŠŽ.¹©Ė®²æĆžąĄėĒĄŠŽ¹¤µŲ15Ē§Ć×.ĒĄŠŽ³µ×°ŌŲ×ÅĖłŠč²ÄĮĻĻČ“Ó¹©Ė®²æĆųö·¢£¬15·ÖÖÓŗ󣬹¤ČĖ³Ė¼ŖĘÕ³µ“ÓĶ¬Ņ»µŲµć³ö·¢£¬½į¹ūĖūĆĒĶ¬Ź±µ½“ļĒĄŠŽ¹¤µŲ£®ŅŃÖŖ¼ŖĘÕ³µĖŁ¶ČŹĒĒĄŠŽ³µĖŁ¶ČµÄ1.5±¶£¬ĒóÕāĮ½ÖÖ³µµÄĖŁ¶Č.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬µćE”¢D”¢F·Ö±šŌŚ±ßAB”¢BC”¢CAÉĻ£¬ĒŅDE”ĪCA£¬DF”ĪBA£®ĻĀĮŠĖÄøöÅŠ¶ĻÖŠ£¬²»ÕżČ·µÄŹĒ£Ø £©
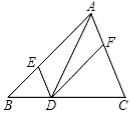
A£®ĖıߊĪAEDFŹĒĘ½ŠŠĖıߊĪ
B£®Čē¹ū”ĻBAC=90”ć£¬ÄĒĆ“ĖıߊĪAEDFŹĒ¾ŲŠĪ
C£®Čē¹ūADĘ½·Ö”ĻBAC£¬ÄĒĆ“ĖıߊĪAEDFŹĒ¾ŲŠĪ
D£®Čē¹ūAD”ĶBCĒŅAB=AC£¬ÄĒĆ“ĖıߊĪAEDFŹĒĮāŠĪ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£ØŠĀÖŖѧĻ°£©
Čē¹ūŅ»øöČż½ĒŠĪÓŠŅ»±ßÉĻµÄÖŠĻßµČÓŚÕāĢõ±ßµÄŅ»°ė£¬ÄĒĆ“ĪŅĆĒ¾Ķ°ŃÕāŃłµÄČż½ĒŠĪ½Š×ö”°ÖĒ»ŪČż½ĒŠĪ”±£®
£Ø¼ņµ„ŌĖÓĆ£©
£Ø1£©ĻĀĮŠČżøöČż½ĒŠĪ£¬ŹĒÖĒ»ŪČż½ĒŠĪµÄŹĒ______£ØĢīŠņŗÅ£©£»

£Ø2£©ČēĶ¼£¬ŅŃÖŖµČ±ßČż½ĒŠĪ![]() £¬ĒėÓĆæĢ¶Č³ßŌŚøĆČż½ĒŠĪ±ßÉĻÕŅ³öĖłÓŠĀś×ćĢõ¼žµÄµć
£¬ĒėÓĆæĢ¶Č³ßŌŚøĆČż½ĒŠĪ±ßÉĻÕŅ³öĖłÓŠĀś×ćĢõ¼žµÄµć![]() £¬Ź¹
£¬Ź¹![]() ĪŖ”°ÖĒ»ŪČż½ĒŠĪ”±£¬²¢Š“³ö×÷·Ø£»
ĪŖ”°ÖĒ»ŪČż½ĒŠĪ”±£¬²¢Š“³ö×÷·Ø£»

£ØÉīČėĢ½¾æ£©
£Ø3£©ČēĶ¼£¬ŌŚÕż·½ŠĪ![]() ÖŠ£¬µć
ÖŠ£¬µć![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬
µÄÖŠµć£¬![]() ŹĒ
ŹĒ![]() ÉĻŅ»µć£¬ĒŅ
ÉĻŅ»µć£¬ĒŅ![]() £¬ŹŌÅŠ¶Ļ
£¬ŹŌÅŠ¶Ļ![]() ŹĒ·ńĪŖ”°ÖĒ»ŪČż½ĒŠĪ”±£¬²¢ĖµĆ÷ĄķÓÉ£»
ŹĒ·ńĪŖ”°ÖĒ»ŪČż½ĒŠĪ”±£¬²¢ĖµĆ÷ĄķÓÉ£»

£ØĮé»īÓ¦ÓĆ£©
£Ø4£©ČēĶ¼£¬µČ±ßČż½ĒŠĪ![]() ±ß³¤
±ß³¤![]() £®Čō¶Æµć
£®Čō¶Æµć![]() ŅŌ
ŅŌ![]() µÄĖŁ¶Č“Óµć
µÄĖŁ¶Č“Óµć![]() ³ö·¢£¬ŃŲ
³ö·¢£¬ŃŲ![]() µÄ±ß
µÄ±ß![]() ŌĖ¶Æ£®ČōĮķŅ»¶Æµć
ŌĖ¶Æ£®ČōĮķŅ»¶Æµć![]() ŅŌ
ŅŌ![]() µÄĖŁ¶Č“Óµć
µÄĖŁ¶Č“Óµć![]() ³ö·¢£¬ŃŲ±ß
³ö·¢£¬ŃŲ±ß![]() ŌĖ¶Æ£¬Į½µćĶ¬Ź±³ö·¢£¬µ±µć
ŌĖ¶Æ£¬Į½µćĶ¬Ź±³ö·¢£¬µ±µć![]() Ź×“Ī»Ųµ½µć
Ź×“Ī»Ųµ½µć![]() Ź±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčŌĖ¶ÆŹ±¼äĪŖ
Ź±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčŌĖ¶ÆŹ±¼äĪŖ![]() £¬ÄĒĆ“
£¬ÄĒĆ“![]() ĪŖ______
ĪŖ______![]() Ź±£¬
Ź±£¬![]() ĪŖ”°ÖĒ»ŪČż½ĒŠĪ”±£®
ĪŖ”°ÖĒ»ŪČż½ĒŠĪ”±£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÕżĪå±ßŠĪµÄ±ß³¤ĪŖ2£¬Į¬½Ó¶Ō½ĒĻßAD£¬BE£¬CE£®Ļ߶ĪAD·Ö±šÓėBE£¬CEĻą½»ÓŚµćM£¬N£®øų³öĻĀĮŠ½įĀŪ£ŗ¢Ł”÷ABM”Õ”÷DCN£»¢ŚDM2=DNAD£»¢ŪMN=3+![]() £»¢ÜĖıߊĪANCBĪŖĮāŠĪ£®ĘäÖŠÕżČ·µÄŹĒ_____
£»¢ÜĖıߊĪANCBĪŖĮāŠĪ£®ĘäÖŠÕżČ·µÄŹĒ_____

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
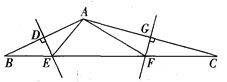
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬AB”¢ACµÄ“¹Ö±Ę½·ÖĻß·Ö±š½»BCÓŚµćE”¢F£®Čō”÷AEFµÄÖܳ¤ĪŖ12cm£¬ŌņBCµÄ³¤ĪŖ____________________cm£®Čō”ĻEAF=110”ć£¬Ōņ”ĻBAC£½_____________________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬A£¬P£¬B£¬CŹĒ°ė¾¶ĪŖ8µÄ”ŃOÉĻµÄĖÄµć£¬ĒŅĀś×ć”ĻBAC=”ĻAPC=60”ć£¬

£Ø1£©ĒóÖ¤£ŗ”÷ABCŹĒµČ±ßČż½ĒŠĪ£»
£Ø2£©ĒóŌ²ŠÄOµ½BCµÄ¾ąĄėOD£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćA1µÄ×ų±źĪŖ£Ø1£¬0£©£¬A2ŌŚyÖįµÄÕż°ėÖįÉĻ£¬ĒŅ”ĻA1A2O =30”ć£¬¹żµćA2×÷A2A3”ĶA1A2£¬“¹×ćĪŖA2£¬½»xÖįÓŚµćA3£»¹żµćA3×÷A3A4”ĶA2A3£¬“¹×ćĪŖA3£¬½»yÖįÓŚµćA4£»¹żµćA4×÷A4A5”ĶA3A4£¬“¹×ćĪŖA4£¬½»xÖįÓŚµćA5£»¹żµćA5×÷A5A6”ĶA4A5£¬“¹×ćĪŖA5£¬½»yÖįÓŚµćA6£»”°““Ė¹ęĀɽųŠŠĻĀČ„£¬ŌņµćA2018µÄׯ×ų±źĪŖ______£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com