
如果一梯子底端离建筑物9 m远,那么15 m长的梯子可达到建筑物的高度是_______m.
12 【解析】【解析】 如图;梯子AC长是15m,梯子底端离建筑物的距离AB长为9m. 在Rt△ABC中,AC=15m,AB=9m. 根据勾股定理,得BC===12m.故答案为:12. 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:单选题
在一个不透明的袋子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中红球的个数约为( )
A. 4个 B. 6个 C. 8个 D. 12个
C 【解析】试题解析:由题意可得: =0.4, 解得:x=8, 故选C查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:解答题
(6分)解方程: 
查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:单选题
将0.00000305用科学记数法表示为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:填空题
如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:单选题
如图,一圆柱高8 cm,底面半径为 cm,一只蚂蚁从点
cm,一只蚂蚁从点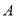 爬到点
爬到点 处吃食,要爬行的最短路程是( )cm.
处吃食,要爬行的最短路程是( )cm.

A. 6 B. 8 C. 10 D. 12
C 【解析】【解析】 底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为: ×2π×=6(cm),展开后的图形中,有BC=8cm,AC=6cm,根据勾股定理得:AB==10(cm).故选C.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:单选题
已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A. 25 B. 14 C. 7 D. 7或25
D 【解析】试题分析:根据直角三角形的性质可得:第三边的平方=-=7或+=25.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
在平面直角坐标系中,△ABC顶点A的坐标为(2,3).若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为 ,则点A′的坐标为( )
,则点A′的坐标为( )
A. (3,  ) B. (3,
) B. (3, 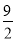 )或(-3,
)或(-3,  )
)
C. ( ,-2) D. (
,-2) D. ( ,2)或(
,2)或(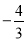 ,-2)
,-2)
查看答案和解析>>
科目:初中数学 来源:山西省吕梁市孝义市2016-2017学年九年级(上)期末考试数学试卷 题型:填空题
在扇形纸片AOB中,∠AOB=90°,OA=4,将扇形纸片AOB按如图所示折叠,使对折后点A与点O重合,折痕为DE,则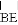 的长度为__________.
的长度为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com