
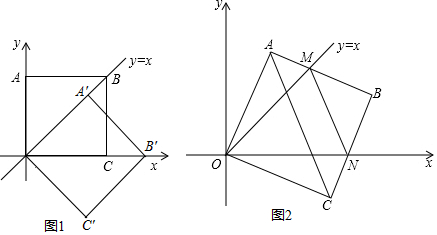
分析 (1)如图1中,作A′H⊥OB′于H.易知△OA′H是等腰直角三角形,点B′在x轴上,由此即可解决问题;
(2)①结论:AM+CN=MN;延长BA交y轴于E点,由△OAE≌△OCN(ASA),推出△OME≌△OMN(SAS),可得MN=ME=AM+AE,推出MN=AM+CN;
②利用①中结论,求出BM、BN、MN,根据△BMN的内切圆半径r=$\frac{BM+BN-MN}{2}$计算即可;
解答 解:(1)如图1中,作A′H⊥OB′于H.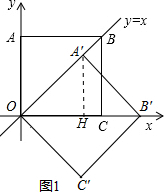
∵四边形ABCD是正方形,
∴OA=OC=BC=AB=2,∠BOC=45°=45,OB=2$\sqrt{2}$,
∵OA′=2,
∴AH=OH=$\sqrt{2}$,
∴A′($\sqrt{2}$,$\sqrt{2}$),
∵旋转角为45°,
∴B′在x轴上,
∴B′(2$\sqrt{2}$,0),
故答案为A′($\sqrt{2}$,$\sqrt{2}$),B′(2$\sqrt{2}$,0);
(2)①结论:AM+CN=MN;
理由:延长BA交y轴于E点,
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON,
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN,
在△OAE和△OCN中,
$\left\{\begin{array}{l}{∠AOE=∠CON}\\{OA=OC}\\{∠EAO=∠NCO=90°}\end{array}\right.$,
∴△OAE≌△OCN(ASA),
∴OE=ON,AE=CN,
在△OME和△OMN中
$\left\{\begin{array}{l}{OE=ON}\\{∠EOM=∠NOM}\\{OM=OM}\end{array}\right.$,
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
②∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM,
∴BM=BN,∵BA=BC,
∴AM=NC,
设AM=NC=a,则MN=2a,
在Rt△BMN中,(2a)2=(2-a)2+(2-a)2,
解得a=2$\sqrt{2}$-2或-2$\sqrt{2}$-2(舍弃),
∴MN=4$\sqrt{2}$-4,BM=BN=4-2$\sqrt{2}$,
∴△BMN的内切圆半径r=$\frac{BM+BN-MN}{2}$=$\frac{4-2\sqrt{2}+4-2\sqrt{2}-(4\sqrt{2}-4)}{2}$=6-4$\sqrt{2}$.
点评 本题考查可知正方形的性质、全等三角形的判定和性质、等腰直角三角形的性质、勾股定理、三角形的内切圆半径等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,记住直角三角形的内切圆的半径,属于中考压轴题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:填空题
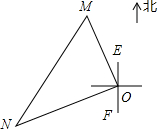 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处.若M,N两点相距100海里,则∠NOF的度数为70°.
一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处.若M,N两点相距100海里,则∠NOF的度数为70°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 80 | 85 | 90 | 95 |
| 人数(人) | 1 | 2 | 5 | 2 |
| A. | 90,89 | B. | 90,90 | C. | 90,90.5 | D. | 90,95 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
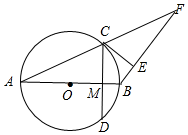 如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.
如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
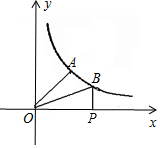 如图,已知A、B是反比例函数y=$\frac{k}{x}$图象上两点,BP⊥x轴,垂足为P.
如图,已知A、B是反比例函数y=$\frac{k}{x}$图象上两点,BP⊥x轴,垂足为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com