
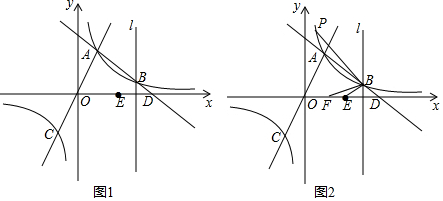
���� ��1����A���������y=$\frac{k}{x}$�п����k��ֵ��
��2�������÷��������������ĶԳ��Եõ�C��-1��-3�����ٰ�B��m��1������y=$\frac{3}{x}$���m�õ�B��3��1����ͨ��ȷ��ֱ��AB�Ľ���ʽ�õ�D��4��0�����������öԳ���ȷ��E��2��0�����������ô���ϵ���������ֱ��BC�Ľ���ʽΪy=x-2��Ȼ���жϵ�E�Ƿ�ֱ��BC�ϣ�
��3��ֱ��AB��y����M��ֱ��BP��y����N����ͼ2����ȷ��M��0��4���������BM=3$\sqrt{2}$��BE=$\sqrt{2}$��EF=$\frac{1}{2}$����֤����BMN�ס�BEF��ͨ�����Ʊȼ����MN=$\frac{3}{2}$���Ӷ��õ�N��0��$\frac{11}{2}$���������ô���ϵ�����õ�ֱ��BN�Ľ���ʽΪy=-$\frac{3}{2}$x+$\frac{11}{2}$��Ȼ��ͨ���ⷽ����$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=-\frac{3}{2}x+\frac{11}{2}}\end{array}\right.$��P�����꣮
��� �⣺��1����A��1��3���ڷ���������y=$\frac{k}{x}$��ͼ���ϣ�
��k=1��3=3��
��2����B��E��C��ͬһ��ֱ���ϣ��������£�
��ֱ��OA�뷴��������y=$\frac{3}{x}$��k��0����ͼ�����һ֧���ڵ�C��
���A���C����ԭ��Գƣ�
��C��-1��-3����
��B��m��1���ڷ���������y=$\frac{3}{x}$��ͼ���ϣ�
��1��m=3�����m=3����B��3��1����
��A��1��3������y=-x+b��-1+b=3�����b=4��
��ֱ��AB�Ľ���ʽΪy=-x+4��
��y=0ʱ��-x+4=0�����x=4����D��4��0����
�ߵ�E���D����ֱ��x=3�Գƣ�
��E��2��0����
��ֱ��BC�Ľ���ʽΪy=px+q��
��B��3��1����C��-1��-3�������$\left\{\begin{array}{l}{3p+q=1}\\{-p+q=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{p=1}\\{q=-2}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=x-2��
��x=2ʱ��y=x-2=0��
���E��ֱ��BC�ϣ�
����B��E��C��ͬһ��ֱ���ϣ�
��3��ֱ��AB��y����M��ֱ��BP��y����N����ͼ2��
��x=0ʱ��y=-x+4=4����M��0��4����
��B��3��1����E��2��0����F��$\frac{3}{2}$��0����
��BM=$\sqrt{{3}^{2}+��1-4��^{2}}$=3$\sqrt{2}$��BE=$\sqrt{��3-2��^{2}+{1}^{2}}$=$\sqrt{2}$��EF=2-$\frac{3}{2}$=$\frac{1}{2}$��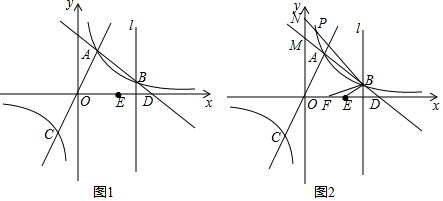
��OM=OD=4��
���OMDΪ����ֱ�������Σ�
���OMD=��ODM=45�㣬
�ߵ�E���D����ֱ��x=3�Գƣ�
���BED=��BDE=45�㣬
���BMN=��BEF=135�㣬
�ߡ�ABP=��EBF��
���BMN�ס�BEF��
��$\frac{MN}{EF}$=$\frac{BM}{BE}$����$\frac{MN}{\frac{1}{2}}$=$\frac{3\sqrt{2}}{\sqrt{2}}$�����MN=$\frac{3}{2}$��
��N��0��$\frac{11}{2}$����
��ֱ��BN�Ľ���ʽΪy=ax+n��
��B��3��1����N��0��$\frac{11}{2}$�������$\left\{\begin{array}{l}{3a+n=1}\\{n=\frac{11}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{n=\frac{11}{2}}\end{array}\right.$��
��ֱ��BN�Ľ���ʽΪy=-$\frac{3}{2}$x+$\frac{11}{2}$��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=-\frac{3}{2}x+\frac{11}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{9}{2}}\end{array}\right.$��
��P��������$\frac{2}{3}$��$\frac{9}{2}$����
�ʴ�Ϊ3��$\frac{2}{3}$��$\frac{9}{2}$��
���� ���⿼���˷������������ۺ��⣺�������շ���������ͼ���ϵ���������������������������ʣ������ô���ϵ��������������һ�κ�������ʽ����ͨ���ⷽ�������ǵĽ������ꣻ���������Ʊȼ����߶εij�������������ͼ�����ʣ���ס�����ľ��빫ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
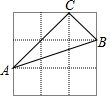 ��ͼ����3��3�������������У�ÿ��С�����εı߳���Ϊ1����ABC������������ڸ���ϣ���AB���ϵĸ�Ϊ��������
��ͼ����3��3�������������У�ÿ��С�����εı߳���Ϊ1����ABC������������ڸ���ϣ���AB���ϵĸ�Ϊ��������| A�� | $\frac{2\sqrt{10}}{5}$ | B�� | $\frac{\sqrt{10}}{5}$ | C�� | $\frac{\sqrt{10}}{10}$ | D�� | $\frac{3\sqrt{10}}{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
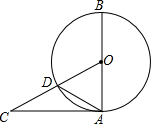 ��ͼ��AB�ǡ�O��ֱ����AC���O���У�CO����O�ڵ�D������CAD=30�㣬���BOD=120�㣮
��ͼ��AB�ǡ�O��ֱ����AC���O���У�CO����O�ڵ�D������CAD=30�㣬���BOD=120�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
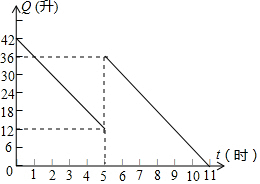 ij����������ǰ����������42������ʻ����Сʱ��;���ڼ���վ������������������������Q����������ʻʱ��t��ʱ��֮��ĺ�����ϵ��ͼ��ʾ���ش��������⣮
ij����������ǰ����������42������ʻ����Сʱ��;���ڼ���վ������������������������Q����������ʻʱ��t��ʱ��֮��ĺ�����ϵ��ͼ��ʾ���ش��������⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��0 | B�� | 0��m��$\frac{1}{2}$ | C�� | m��$\frac{1}{2}$ | D�� | m��$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
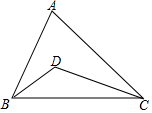 ��ͼ���ڡ�ABC�У���A=70�㣬D�ǡ�ABC��һ�㣬����ABD=30�㣬��ACD=25�㣬���BDC=125�㣮
��ͼ���ڡ�ABC�У���A=70�㣬D�ǡ�ABC��һ�㣬����ABD=30�㣬��ACD=25�㣬���BDC=125�㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com