
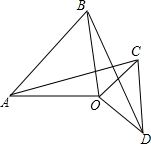
 如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°,当将△COD绕点O顺时针旋转时,连线AC与BD之间的大小关系如何?试猜想并证明你的结论.
如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°,当将△COD绕点O顺时针旋转时,连线AC与BD之间的大小关系如何?试猜想并证明你的结论.  一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
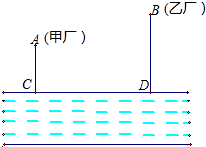 如图,在河流的一侧有甲、乙两个工厂,它们各有一条垂直于江边的小路,长度分别为4千米和5千米,若两条小路相距18千米,现要在江边建立一个抽水站,把水送到甲、乙两厂去,要使供水管长度之和最短,抽水站应建在哪里?
如图,在河流的一侧有甲、乙两个工厂,它们各有一条垂直于江边的小路,长度分别为4千米和5千米,若两条小路相距18千米,现要在江边建立一个抽水站,把水送到甲、乙两厂去,要使供水管长度之和最短,抽水站应建在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方程两根之和是1 | B. | 方程两根之积是3 | ||
| C. | 方程两根之平方和是7 | D. | 方程两根倒数之和是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
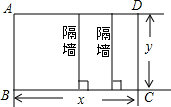 某工厂拟建一座平面图形是矩形且面积为200m2的三级污水处理池(如图所示),由于受地形限制,污水处理池的长与宽都不得超过16m,设污水处理池的一边长为xm,另一边长为ym.
某工厂拟建一座平面图形是矩形且面积为200m2的三级污水处理池(如图所示),由于受地形限制,污水处理池的长与宽都不得超过16m,设污水处理池的一边长为xm,另一边长为ym.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
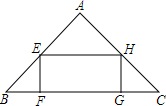 如图,在一个直角边长为4cm的等腰直角三角形内部,截出一个矩形EFGH,设EF的长为x cm,矩形的面积为y cm2.
如图,在一个直角边长为4cm的等腰直角三角形内部,截出一个矩形EFGH,设EF的长为x cm,矩形的面积为y cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
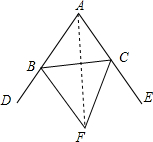 如图,△ABC的外角∠CBD,∠BCE的平分线相交于点F,求证:
如图,△ABC的外角∠CBD,∠BCE的平分线相交于点F,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com