练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，在等边三角形ABC中，AB=2，点D为BC的中点，DE∥AB交AC于点E，过点E作EF⊥DE，交BC的延长线于点F，则图中长度为1的线段有（　　）
    A．3条B．4条C．5条D．6条

    分析 根据等边三角形的性质进行解答即可．

    解答 解：∵等边三角形ABC中，AB=2，点D为BC的中点，DE∥AB，
    ∴图中长度为1的线段有BD，DC，DE，AE，EC，CF，
    故选D

    点评 此题考查了等边三角形的性质．此题难度不大，注意掌握数形结合思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．某超市销售一种饮料，平均每天可售出100箱，每箱利润为120元，为了扩大销量，尽快减少库存，超市准备适当降价，据测算，若每箱降价2元，则每天可多售出4箱．
    （1）如果要使每天销售该饮料获利14000元，则每箱应降价多少元．
    （2）每天销售该饮料获利能达到14500元吗？若能，则每箱应降价多少？若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的“探究”
    【提出问题】三个有理数a、b、c满足abc＞0，求$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的值．
    【解决问题】
    解：由题意得：a，b，c三个有理数都为正数或其中一个为正数，另两个为负数．
    ①当a，b，c都是正数，即a＞0，b＞0，c＞0时，
    则：$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=$\frac{a}{a}$+$\frac{b}{b}$+$\frac{c}{c}$=1+1+3；②当a，b，c有一个为正数，另两个为负数时，设a＞0，b＜0，c＜0，
    则：$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=$\frac{a}{a}$+$\frac{-b}{b}$+$\frac{-c}{c}$=1-1-1=-1
    所以：$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的值为3或-1．
    【探究】请根据上面的解题思路解答下面的问题：
    （1）三个有理数a，b，c满足abc＜0，求$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的值；
    （2）已知|a|=3，|b|=1，且a＜b，求a+b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）（$\frac{1}{2}$）-1-2+（π-3.14）0     
    （2）$\frac{{x}^{2}-1}{{x}^{2}+2x+1}$÷$\frac{{x}^{2}-x}{x+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．若扇形OAB的圆心角为120°，半径为3，则该扇形的弧长为2π．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列对函数的认识正确的是（　　）
    A．若y是x的函数，那么x也是y的函数
    B．两个变量之间的函数关系一定能用数学式子表达
    C．若y是x的函数，则当y取一个值时，一定有唯一的x值与它对应
    D．一个人的身高也可以看作他年龄的函数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知反比例函数y=$\frac{k}{x}$的图象与直线y=x+1都过点（-3，n）
    （1）求n，k的值；
    （2）若抛物线y=x2-2mx+m2-m-1的顶点在反比例函数y=$\frac{k}{x}$的图象上，求这条抛物线的顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．分式方程$\frac{2}{x+1}$=$\frac{1}{x-1}$的解为x=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

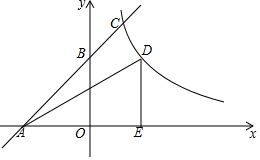    6．在平面直角坐标系内，点O为坐标原点，直线y=x+4交x轴于点A，交y轴于点B，点C（2，m）在直线y=x+4上，反比例函数
    y=$\frac{n}{x}$经过点C．
    （1）求m，n的值；
    （2）点D在反比例函数y=$\frac{n}{x}$的图象上，过点D作X轴的垂线，点E为垂足，若OE=3，连接AD，求tan∠DAE的值．

    查看答案和解析>>

    同步练习册答案