
【题目】如图是一块含30°(即∠CAB=30°)角的三角板和一个量角器拼在一起,三角板斜边AB与量角器所在圆的直径MN重合,其量角器最外缘的读数是从N点开始(即N点的读数为0),现有射线CP绕着点C从CA顺时针以每秒2度的速度旋转到与△ACB外接圆相切为止.在旋转过程中,射线CP与量角器的半圆弧交于E.
(1)当射线CP与△ABC的外接圆相切时,求射线CP旋转度数是多少?
(2)当射线CP分别经过△ABC的外心、内心时,点E处的读数分别是多少?
(3)当旋转7.5秒时,连接BE,求证:BE=CE.
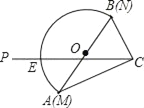
【答案】(1)射线CP旋转度数是120°;(2)E处的读数为90;(3)证明见解析.
【解析】
(1) 连接OC. 根据切线的性质, 得∠OCP=![]() , 根据等腰三角形的性质,得∠ACO=∠A, 从而求得射线CP旋转度数;
, 根据等腰三角形的性质,得∠ACO=∠A, 从而求得射线CP旋转度数;
(2) 当CP过△ABC外心时 (即过O点)时,∠BCE=![]() , 根据圆周角定理, 则点E处的读数是
, 根据圆周角定理, 则点E处的读数是![]() ;当CP过△ABC的内心时, 即CP平分∠ACB, 则∠BCE=
;当CP过△ABC的内心时, 即CP平分∠ACB, 则∠BCE=![]() , 根据圆周角定理,则点E处的读数是
, 根据圆周角定理,则点E处的读数是![]() .
.
(3) 根据已知, 知旋转了![]() , 即可求得∠EBC=∠BCE=
, 即可求得∠EBC=∠BCE=![]() , 从而证明结论.
, 从而证明结论.
(1)连接OC.
∵射线CP与△ABC的外接圆相切,
∴∠OCP=90°,
∵OA=OC,
∴∠ACO=∠A=30°,
∴射线CP旋转度数是120°;
(2) 
∵∠BCA=90°,
∴△ABC的外接圆就是量角器所在的圆.
当CP过△ABC外心时(即过O点),∠BCE=60°,
∴∠BOE=120°,即E处的读数为120,
当CP过△ABC的内心时,∠BCE=45°,∠EOB=90°,
∴E处的读数为90.
(3)在图2中,
∵∠PCA=2×7.5°=15°,∠BCE=75°,∠ECA=∠EBA=15°,
∴∠EBC=∠EBA+∠ABC=∠BCE=75°,
∴BE=EC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P0的坐标为(2,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
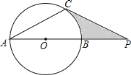
【题目】如图,已知:![]() 的直径
的直径![]() 与弦
与弦![]() 的夹角
的夹角![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 的直径是
的直径是![]() ,以点
,以点![]() 为圆心作圆,当半径为多长时,
为圆心作圆,当半径为多长时,![]() 与
与![]() 相切?
相切?
![]() 若
若![]() ,求图中阴影部分的面积(结果精确到
,求图中阴影部分的面积(结果精确到![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,长沙开始推广垃圾分类,分类垃圾桶成为我们生活中的必备工具.某学校开学初购进![]() 型和
型和![]() 型两种分类垃圾桶,购买
型两种分类垃圾桶,购买![]() 型垃圾桶花费了2500元,购买
型垃圾桶花费了2500元,购买![]() 型垃圾桶花费了2000元,且购买
型垃圾桶花费了2000元,且购买![]() 型垃圾桶数量是购买
型垃圾桶数量是购买![]() 型垃圾桶数量的2倍,已知购买一个
型垃圾桶数量的2倍,已知购买一个![]() 型垃圾桶比购买一个
型垃圾桶比购买一个![]() 型垃圾桶多花30元.
型垃圾桶多花30元.
(1)求购买一个![]() 型垃圾桶、B型垃圾桶各需多少元?
型垃圾桶、B型垃圾桶各需多少元?
(2)由于实际需要,学校决定再次购买分类垃圾桶,已知此次购进![]() 型和
型和![]() 型两种分类垃圾桶的数量一共为50个,恰逢市场对这两种垃圾桶的售价进行调整,
型两种分类垃圾桶的数量一共为50个,恰逢市场对这两种垃圾桶的售价进行调整,![]() 型垃圾桶售价比第一次购买时提高了8%,
型垃圾桶售价比第一次购买时提高了8%,![]() 型垃圾桶按第一次购买时售价的9折出售,如果此次购买
型垃圾桶按第一次购买时售价的9折出售,如果此次购买![]() 型和
型和![]() 型这两种垃圾桶的总费用不超过3240元,那么此次最多可购买多少个
型这两种垃圾桶的总费用不超过3240元,那么此次最多可购买多少个![]() 型垃圾桶?
型垃圾桶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)如图1,E为线段DC上任意一点,将线段![]() 绕点D逆时针旋转90°得到线段
绕点D逆时针旋转90°得到线段![]() ,连接
,连接![]() ,过点F作
,过点F作![]() ,交直线
,交直线![]() 于点
于点![]() .判断
.判断![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)如图2,若![]() 为线段
为线段![]() 的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.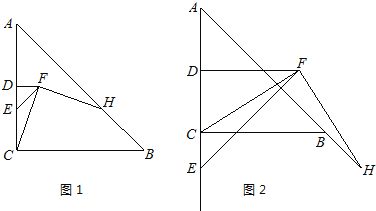
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米![]()
(1)设平均每天的工作量为x(单位:万米![]() ),用
),用![]() 来表示运输公司完成任务所需的时间,并写出x的取值范围.
来表示运输公司完成任务所需的时间,并写出x的取值范围.
(2)由于工程进度的需要,实际平均每天运送土石方是原计划的1.2倍,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少米![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com