
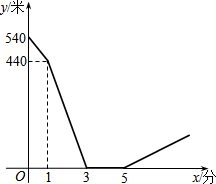
 小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:分析 (1)由图象可以看出,0-1min内,小刚的速度可由距离减小量除以时间求得,1-3min内,根据等量关系“距离减小量=小刚跑过的路程+小强跑过的路程”可得出小强的速度;
(2)根据小刚的速度始终是180米/分,小强的速度始终是220米/分,则他们的速度之差是40米/分,设y与x之间的函数关系式为y=40x+b.将(5,0)代入得b=-200,所以y=40x-200.
(3)先由y与x之间的函数关系式算出15分钟后(由于图象是小刚出家门开始计时的)两人之间的距离,再根据等量关系“相遇时小刚跑过的距离+小强跑过的距离=二人之间的距离”列出方程求解即可.
解答 解:(1)小刚比赛前的速度:${v}_{1}=\frac{540-440}{1}$=100(米/分),
小强比赛前的速度,由2×(v1+v2)=440,得v2=120米/分.
故答案为:100,120;
(2)∵小刚的速度始终是180米/分,小强的速度始终是220米/分,
他们的速度之差是40米/分,
∴设y与x之间的函数关系式为y=40x+b.
将(5,0)代入得b=-200
∴y=40x-200.
(3)当x=5+10=15时,y=400.
设再经过t分钟两人相遇,
180t+220t=400,
解得:t=1.
答:再经过1分钟两人相遇.
点评 本题是一道关于行程问题的一次函数试题,考查了行程问题的数量关系的运用,相遇问题,追击问题的综合运用,解答时灵活运用行程问题的数量关系解答是关键.


科目:初中数学 来源: 题型:填空题
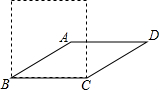 如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
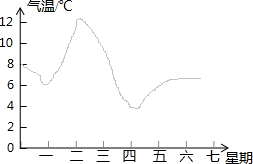 某市一周平均气温(℃)如图所示,下列说法不正确的是( )
某市一周平均气温(℃)如图所示,下列说法不正确的是( )| A. | 星期二的平均气温最高 | B. | 星期四到星期日天气逐渐转暖 | ||
| C. | 这一周最高气温与最低气温相差4℃ | D. | 星期四的平均气温最低 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数 y1=$\frac{m}{x}$(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,4)与点A,且与反比例函数的图象相交于另一点B.
如图,已知反比例函数 y1=$\frac{m}{x}$(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,4)与点A,且与反比例函数的图象相交于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
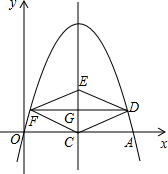 如图,在平面直角坐标系中,二次函数y=-x2+bx的图象经过点A(4,0).点E是过点C(2,0)且与y轴平行的直线上的一个动点,过线段CE的中点G作DF⊥CE交二次函数的图象于D、F两点.
如图,在平面直角坐标系中,二次函数y=-x2+bx的图象经过点A(4,0).点E是过点C(2,0)且与y轴平行的直线上的一个动点,过线段CE的中点G作DF⊥CE交二次函数的图象于D、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=x-2图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(3,m),与x轴交于点B.
如图,一次函数y=x-2图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(3,m),与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
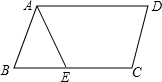 如图,在?ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( )
如图,在?ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( )| A. | 8cm | B. | 6cm | C. | 4cm | D. | 2cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com