
【题目】杨辉是我国南宋时期杰出的数学家和教育家,下图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
(1)图中给出了七行数字,根据构成规律,第8行中从右边数第4个数是_______;
(2)利用不完全归纳法探索出第![]() 行中的所有数字之和为_________.
行中的所有数字之和为_________.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合我市“富美乡村建设”宣传活动,某社区对“推动富美乡村建设的政策与举措的了解情况”进行问卷调查,问卷中把了解情况分为“非常了解(A)”、“有些了解(B)”、“不了解(C)”三类,并将调查结果分析整理后,制成如图所示的两个统计图.
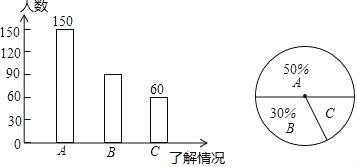
请根据以上两幅图的信息解答下列问题:
(1)这次调查活动共调查了_____人,其中“有些了解(B)”有_____人;
(2)在扇形统计图中,“B”所对应的扇形的圆心角度数是多少?
(3)如果该社区共有居民5000人,试估计“不了解(C)”的居民人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
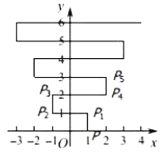
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() .点
.点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位至点
,第3次向上跳动1个单位至点![]() ,第4次向右跳动3个单位至点
,第4次向右跳动3个单位至点![]() ,第5次又向上跳动1个单位至点
,第5次又向上跳动1个单位至点![]() ,第6次向左跳动4个单位至点
,第6次向左跳动4个单位至点![]() ,……,照此规律,点
,……,照此规律,点![]() 第2020次跳动至点
第2020次跳动至点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法
解:∵x﹣y=2,∴x=y+2 又∵x>1∴y+2>1∴y>﹣1
又∵y<0∴﹣1<y<0…①
同理可得1<x<2…②
由①+②得:﹣1+1<x+y<0+2∴x+y的取值范围是0<x+y<2
按照上述方法,完成下列问题:
(1)已知x﹣y=3,且x>2,y<1,则x+y的取值范围是
(2)已知关于x,y的方程组![]() 的解都是正数
的解都是正数
①求a的取值范围;②若a﹣b=4,求a+b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
①![]() 的解x= .
的解x= .
②![]() 的解x= .
的解x= .
③![]() 的解x= .
的解x= .
④![]() 的解x= .
的解x= .
…
(1)根据你发现的规律直接写出⑤,⑥个方程及它们的解.
(2)请你用一个含正整数n的式子表示上述规律,并求出它的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com