
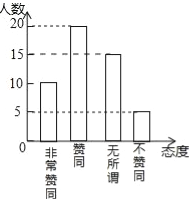
【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题:
(1)在这次问卷调查中一共抽取了 名学生,a= %;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为 度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.

【答案】(1)50,37.5%;(2)详见解析;(3)36°;(4)1800.
【解析】
试题分析:(1)由赞同的人数除以赞同的人数所占的百分比,即可求出样本容量,再求出无所谓态度的人数,进而求出a的值;(2)由(1)可知无所谓态度的人数,将条形统计图补充完整即可;(3)求出不赞成人数的百分数,即可求出圆心角的度数;(4)求出“赞同”和“非常赞同”两种态度的人数所占的百分比,用样本估计总体的思想计算即可.
试题解析:(1)20÷40%=50(人),无所谓态度的人数为50﹣10﹣20﹣5=15,则a=![]() ×100%=37.5%;
×100%=37.5%;
(2)补全条形统计图如图所示:
(3)不赞成人数占总人数的百分数为![]() ×100%=10%,
×100%=10%,
持“不赞同”态度的学生人数的百分比所占扇形的圆心角为10%×360°=36°,
(4)“赞同”和“非常赞同”两种态度的人数所占的百分数为![]() ×100%=60%,
×100%=60%,
则该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和为3000×60%=1800人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
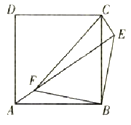
【题目】如图,点E是边长为5的正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.若EF=6,则CF的长为( )
A. 6 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】闵行区政府为残疾人办实事,在道路改造工程中为盲人修建一条长3000米的盲道,根据规划设计和要求,某工程队在实际施工中增加了施工人员,每天修建的盲道比原计划多250米,结果提前2天完成工程,问实际每天修建盲道多少米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数 | 质量等级 | 天数(天) |
0﹣50 | 优 | m |
51﹣100 | 良 | 44 |
101﹣150 | 轻度污染 | n |
151﹣200 | 中度污染 | 4 |
201﹣300 | 重度污染 | 2 |
300以上 | 严重污染 | 2 |
(1 )统计表中m= ,n= .扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天?
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列多面体,并把下表补充完整.
名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
图形 |
|
|
|
|
顶点数a | 6 | 10 | 12 | |
棱数b | 9 | 12 | ||
面数c | 5 | 8 |
(1)完成上表中的数据
(2)根据上表中的规律判断,十四棱柱共有 个面,共有 个顶点,共有 条棱;
(3)若某个棱柱由30个面构成,则这个棱柱为 棱柱;
(4)观察上表中的结果,你能发现顶点数棱数面数之间有什么关系吗?请写出来。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角是 °;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com