Question

11．在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．
（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；
（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF²=ME²+NF²；
（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．

Answer 1

分析 （1）根据旋转的性质可知AF=AG，∠EAF=∠GAE=45°，故可证△AEG≌△AEF；
（2）将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．由（1）知△AEG≌△AEF，则EG=EF．再由△BME、△DNF、△CEF均为等腰直角三角形，得出CE=CF，BE=BM，NF=$\sqrt{2}$DF，然后证明∠GME=90°，MG=NF，利用勾股定理得出EG²=ME²+MG²，等量代换即可证明EF²=ME²+NF²；
（3）延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，结合勾股定理以及相等线段可得（GH+BE）²+（BE-GH）²=EF²，所以2（DF²+BE²）=EF²．

解答 （1）证明：∵△ADF绕着点A顺时针旋转90°，得到△ABG，
∴AF=AG，∠FAG=90°，
∵∠EAF=45°，
∴∠GAE=45°，
在△AGE与△AFE中，
$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE=45°}\\{AE=AE}\end{array}\right.$，
∴△AGE≌△AFE（SAS）；

（2）证明：设正方形ABCD的边长为a．
将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．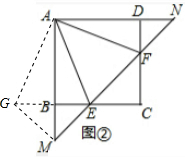
则△ADF≌△ABG，DF=BG．
由（1）知△AEG≌△AEF，
∴EG=EF．
∵∠CEF=45°，
∴△BME、△DNF、△CEF均为等腰直角三角形，
∴CE=CF，BE=BM，NF=$\sqrt{2}$DF，
∴a-BE=a-DF，
∴BE=DF，
∴BE=BM=DF=BG，
∴∠BMG=45°，
∴∠GME=45°+45°=90°，
∴EG²=ME²+MG²，
∵EG=EF，MG=$\sqrt{2}$BM=$\sqrt{2}$DF=NF，
∴EF²=ME²+NF²；

（3）解：EF²=2BE²+2DF²．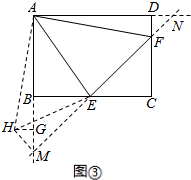
如图所示，延长EF交AB延长线于M点，交AD延长线于N点，
将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．
由（1）知△AEH≌△AEF，
则由勾股定理有（GH+BE）²+BG²=EH²，
即（GH+BE）²+（BM-GM）²=EH²
又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）²+（BE-GH）²=EF²，
即2（DF²+BE²）=EF²

点评 本题是四边形综合题，其中涉及到正方形的性质，旋转的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，矩形的性质，勾股定理．准确作出辅助线利用数形结合及类比思想是解题的关键．