
【题目】如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )

A.9 B.10 C.3![]() D.2
D.2![]()
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
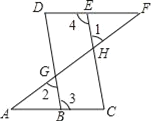
解:∵∠1=∠2(已知)
∠2=∠DGF
∴∠1=∠DGF(____________)
∴BD∥CE
∴∠3+∠C=180°( )
又∵∠3=∠4(已知)
∴∠4+∠C=180°
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,他手中持有的钱数(含备用零钱)y与售出的土豆千克数x的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是______元,降价前他每千克土豆出售的价格是______元;
(2)降价后他按每千克0.8元将剩余土豆售完,这时他手中的钱(含备用零钱)是62元,求降价后的线段所表示的函数表达式并写出它的取值范围.
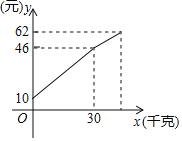
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
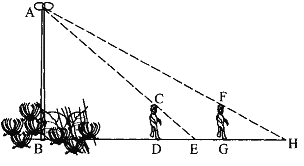
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为_____________.
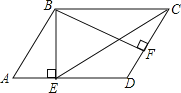
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
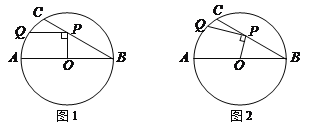
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
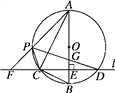
【题目】如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是![]() 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:△PAC∽△PDF;
(2)若AB=5,![]() ,求PD的长;
,求PD的长;
(3)在点P运动过程中,设![]() =x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)
=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
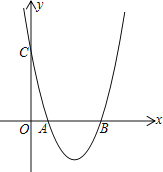
【题目】如图1,抛物线y=x2+bx+c与x轴交于A(1,0)、B(4,0),与y轴交于点C
(1) 求抛物线的解析式
(2) 抛物线上一点D,满足S△DAC=S△OAC,求点D的坐标
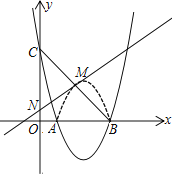
(3) 如图2,已知N(0,1),将抛物线在点A、B之间部分(含点A、B)沿x轴向上翻折,得到图T(虚线部分),点M为图象T的顶点.现将图象保持其顶点在直线MN上平移,得到的图象T1与线段BC至少有一个交点,求图象T1的顶点横坐标的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知![]() 中,
中,![]() ,一条直角边为3,如果
,一条直角边为3,如果![]() 是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com