
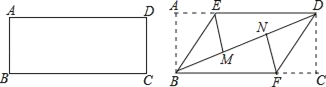
【题目】准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,BE=2,求菱形BFDE的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据矩形的性质和翻折变换的性质得到∠EBD=∠FDB,证明EB∥DF,根据平行四边形的判定定理证明结论;
(2)根据菱形的性质和翻折变换的性质求出∠ABE=30°,根据直角三角形的性质求出AB=![]() ,根据菱形的面积公式计算即可.
,根据菱形的面积公式计算即可.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
由翻折变换的性质可知,∠ABE=∠EBD,∠CDF=∠FDB,
∴∠EBD=∠FDB,
∴EB∥DF,
∵ED∥BF,
∴四边形BFDE为平行四边形;
(2)解:∵四边形BFDE为菱形,
∴∠EBD=∠FBD,
∵∠EBD=∠ABE,
∴∠EBD=∠FBD=∠ABE,
∵四边形ABCD是矩形,
∠ABC=90°,
∴∠EBD=∠FBD=∠ABE=30°,
∴AB=![]() ,
,
∴菱形BFDE的面积S=DE×AB=2![]() .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
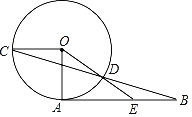
【题目】如图,AB是⊙O的切线,OA,OC是⊙O的半径,且OC∥AB,连接BC交⊙O于点D,点D恰为BC的中点,连接OD并延长,交AB于点E.
(1)求∠B的度数;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,某地的计价规则如表:
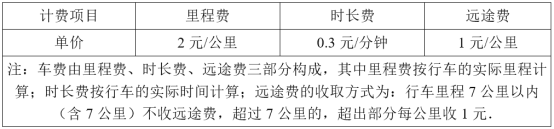
小李与小张分别从不同地点,各自同时乘坐滴滴快车,到同一地点相见,已知到达约定地点时他们的实际行车里程分别为7公里与9公里,两人付给滴滴快车的乘车费相同.其中一人先到达约定地点,他等候另一人的时间等于他自己实际乘车时间,且恰好是另一人实际乘车时间的一半,则小李的乘车费为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
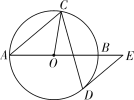
A.65°B.30°C.25°D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
会员卡类型 | 办卡费用/元 | 有效期 | 优惠方式 |
A类 | 40 | 1年 | 每杯打九折 |
B类 | 80 | 1年 | 每杯打八折 |
C类 | 130 | 1年 | 一次性购买2杯,第二杯半价 |
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费![]() 元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )
元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员卡
C.购买C类会员卡D.不购买会员卡
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求c的值;
(2)当![]() 时,求抛物线顶点的坐标;
时,求抛物线顶点的坐标;
(3)已知点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个公共点,结合函数图象,求a的取值范围.
有两个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
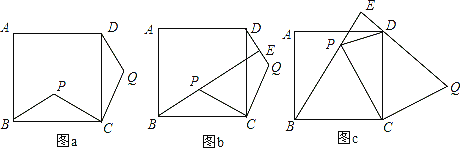
(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
①2019年10月至2020年3月通话时长统计表
时间 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
时长(单位:分钟) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月与2020年5月,这两个月通话时长的总和为1100分钟根据以上信息,推断张老师这八个月的通话时长的中位数可能的最大值为( )
A.550B.580C.610D.630
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com