
【题目】如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )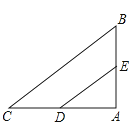
A.相切
B.相交
C.相离
D.无法确定
【答案】B
【解析】解答:过点A作AM⊥BC于点M,交DE于点N,
∴AM×BC=AC×AB,
∴AM=(3×4 )÷5= ![]()
∵D、E分别是AC、AB的中点,
∴DE∥BC,DE= ![]() BC=2.5,
BC=2.5,
∴AN=MN= ![]() AM,
AM,
∴MN=1.2,
∵以DE为直径的圆半径为1.25,
∴r=1.25>1.2,
∴以DE为直径的圆与BC的位置关系是:相交.
故选B.故选:B.
首先过点A作AM⊥BC,根据三角形面积求出AM的长,进而得出直线BC与DE的距离,进而得出直线与圆的位置关系.
【考点精析】本题主要考查了三角形的面积和三角形中位线定理的相关知识点,需要掌握三角形的面积=1/2×底×高;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像交于
)的图像交于
![]() 两点.
两点.
(1)求反比例函数的表达式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求满足条件的点
的值最小,求满足条件的点![]() 的坐标;
的坐标;
(3)在(2)的条件下求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,平面直角坐标系中,O为原点,点A坐标为(﹣4,0),AB∥y轴,点C在y轴上,一次函数y=![]() x+3的图象经过点B、C.
x+3的图象经过点B、C.

(1)点C的坐标为_____,点B的坐标为_____;
(2)如图②,直线l经过点C,且与直线AB交于点M,O'与O关于直线l对称,连接CO'并延长,交射线AB于点D.
①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
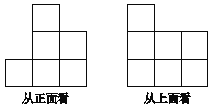
【题目】用大小相同的小立方块搭成一个几何体,使得从正面和上面看到的几何体的形状图如图19所示.
(1)这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
(2)画出这两种情况下从左面看到的几何体的形状图.(各画出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【题目】如图,两个反比例函数C1:y=![]() 和C2:y=
和C2:y=![]() 在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1- k2;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点

A. ①② B. ②④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,且a,c满足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)画出数轴,并把A,B,C三点表示在数轴上;
(3)P是数轴上任意一点,点P表示的数是x,当PA+PB+PC=10时,x的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,第一个图2条直线相交最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交最多有6个交点,…,像这样,则20条直线相交最多交点的个数是( )
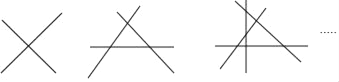
A. 171 B. 190 C. 210 D. 380
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com