
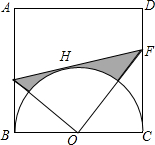
 如图,正方形ABCD的边长为2a,以BC为直径在正方形内作半圆O,H是该半圆上一点,过点H作半圆的切线交AB、CD于E、F.
如图,正方形ABCD的边长为2a,以BC为直径在正方形内作半圆O,H是该半圆上一点,过点H作半圆的切线交AB、CD于E、F.分析 (1)根据切线长定理证明周长为定值;
(2)连接OH,根据切线长定理得出∠BEO=∠OEF=60°,∠CFO=∠EFO=30°,得出BE=$\frac{\sqrt{3}}{3}$a,CF=$\sqrt{3}$a,OE=$\frac{2\sqrt{3}}{3}$a,OF=2a,∠EOF=90°,然后根据S阴影=S-S扇形=$\frac{1}{2}$×OE×OF-$\frac{90π×{a}^{2}}{360}$即可求得.
解答 解:(1)∵BE、EH切半圆O于B、H,
∴BE=EH,
同理,CF=FH,
∴四边形AEFD的周长=AD+AE+EF+FD=AD+(AE+BE)+(DF+CF)=AD+AB+DC=2a+2a+2a=6a,
∴四边形AEFD的周长始终是6a,没有发生变化.
(2)连接OH,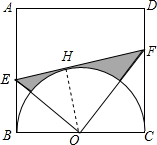
∵EF切半圆O于H,
∴OH⊥EF,BO=CO=OH=a,
∵∠BEF=120°,AB∥CD,
∴∠EFC=60°
∴∠BEO=∠OEF=60°,∠CFO=∠EFO=30°,
∴BE=$\frac{\sqrt{3}}{3}$a,CF=$\sqrt{3}$a,OE=$\frac{2\sqrt{3}}{3}$a,OF=2a,
∵∠OEF=60°,∠EFO=30°,
∴∠EOF=90°,
∴在RT△EOF中,S=$\frac{1}{2}$×OE×OF=$\frac{2\sqrt{3}}{3}$a2,
∴S阴影=S-S扇形=$\frac{2\sqrt{3}}{3}$a2-$\frac{90π×{a}^{2}}{360}$=$\frac{8\sqrt{3}-3π}{12}$a2.
点评 此题是圆的综合题,考查了切线的性质、切线长定理、直角三角形的判定、直角三角形的面积、扇形的面积等知识点,综合性较强,难度偏上.


科目:初中数学 来源: 题型:解答题
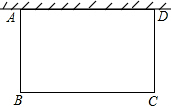 小明和小强利用假期去农场参加社会实践,正遇到农场拟建一个养鸡场,养鸡场的一面靠墙(墙足够长),计划中的建筑材料可建围墙的总长为100m.小明将鸡场设计成矩形,并算出鸡场的面积为1200m2,请你求出此时鸡场的长和宽分别是多少米?
小明和小强利用假期去农场参加社会实践,正遇到农场拟建一个养鸡场,养鸡场的一面靠墙(墙足够长),计划中的建筑材料可建围墙的总长为100m.小明将鸡场设计成矩形,并算出鸡场的面积为1200m2,请你求出此时鸡场的长和宽分别是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
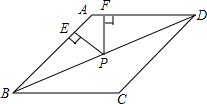 如图,在菱形ABCD中,AB=4,∠A=120°,点P在对角线BD上,PE⊥AB于点E,PF⊥AD于点F,则PE+PF=2$\sqrt{3}$.
如图,在菱形ABCD中,AB=4,∠A=120°,点P在对角线BD上,PE⊥AB于点E,PF⊥AD于点F,则PE+PF=2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
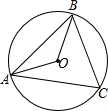 如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )| A. | 50$\sqrt{3}$ | B. | $\frac{100}{3}$$\sqrt{3}$ | C. | $\frac{200}{3}$$\sqrt{3}$ | D. | 200$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com