
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式利用减法法则变形,计算即可得到结果;
(3)原式利用减法法则变形,计算即可得到结果;
(4)原式利用同号两数相加的法则计算即可得到结果;
(5)原式利用减法法则变形,计算即可得到结果;
(6)原式利用减法法则变形,计算即可得到结果;
(7)原式结合后,相加即可得到结果;
(8)原式利用减法法则及绝对值的代数意义变形,计算即可得到结果.
解答 解:(1)-7-(-21)=-7+21=14;
(2)(-38)-(-24)-(+65)=-38+24-65=-79;
(3)13+7-(-20)-(-40)-627=13+7+20+40-627=-547;
(4)-18+(-7)-32=-18-7-32=-57;
(5)(-12)-5+(-14)-(-39)=-12-5-14+39=8;
(6)3$\frac{1}{2}$-(-$\frac{1}{3}}$)+2$\frac{2}{3}$+(-$\frac{1}{2}$)=3$\frac{1}{2}$-$\frac{1}{2}$+$\frac{1}{3}$+2$\frac{2}{3}$=3+3=6;
(7)0.5+(-$\frac{1}{4}$)-2.75+(-$\frac{1}{2}$)=$\frac{1}{2}$-$\frac{1}{2}$-0.25-2.75=-3;
(8)$\frac{2}{5}$-|-1$\frac{1}{2}}$|-(+2$\frac{1}{4}$)-(-2.75)=$\frac{2}{5}$-1$\frac{1}{2}$-2$\frac{1}{4}$+2.75=-$\frac{3}{5}$.
点评 此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
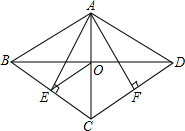 如图 在?ABCD中 对角线AC、BD 相交于点O,AE⊥BC,AF⊥CD,垂足分别是E、F,点E、F恰好为BC、CD的中点,连接OE.
如图 在?ABCD中 对角线AC、BD 相交于点O,AE⊥BC,AF⊥CD,垂足分别是E、F,点E、F恰好为BC、CD的中点,连接OE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
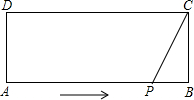 如图,在矩形ABCD中,AB=7cm,BC=$\sqrt{2}$cm,点P从点A出发以1cm/s的速度移动到点B.点P出发$\frac{28-2\sqrt{43}}{3}$秒后,PA=2PC.
如图,在矩形ABCD中,AB=7cm,BC=$\sqrt{2}$cm,点P从点A出发以1cm/s的速度移动到点B.点P出发$\frac{28-2\sqrt{43}}{3}$秒后,PA=2PC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com