
 “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BC=CD=20m.
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BC=CD=20m.分析 (1)求出∠DCA的度数,再判断出BC=CD,据此即可判断出△BCD是等边三角形.
(2)过点B作BE垂直于AD,垂足为E,求出∠DAC的度数,判断出△BCD是等边三角形,再利用三角函数求出AB的长,从而得到AB+BC+CD的长.
解答 (1)证明:由题意可知∠DCA=180°-75°-45°=60°,
∵BC=CD,
∴△BCD是等边三角形.
(2)解:过点B作BE垂直于AD,垂足为E,
由题意可知∠DAC=75°-30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60° BD=BC=CD=20m,
∴∠ADB=∠DBC-∠DAC=15°,
∴BE=sin15°BD≈0.26×20≈5m,
∴AB=$\frac{BE}{sin45°}$=5$\sqrt{2}$≈1.4×5≈7m,
∴AB+BC+CD≈7+20+20≈47m.
答:从A地跑到D地的路程47m.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
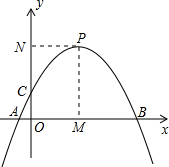 如图,开口向下的抛物线y=a(x-2)2+k,交x轴于点A、B(点A在点B左侧),交y轴正半轴于点C,顶点为P,过顶点P,作x轴,y轴的垂线,垂足分别为M,N.
如图,开口向下的抛物线y=a(x-2)2+k,交x轴于点A、B(点A在点B左侧),交y轴正半轴于点C,顶点为P,过顶点P,作x轴,y轴的垂线,垂足分别为M,N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com