
分析 (1)先证明AE是△FBD的中位线,得出AE∥BD,即AC∥BD,再由已知条件DC∥AB,即可得出结论;
(2)作FG⊥DC交DC延长线于G,先证明△FDG是等腰直角三角形,得出FG=DG,设CG为x,则FG=DG=4+x,再根据勾股定理求出x,得出FG,即可求出△CDF的面积.
解答 (1)证明:∵点A、E分别是边FB、FD的中点,
∴AE是△FBD的中位线,
∴AE∥BD,即AC∥BD,
又∵DC∥AB,
∴四边形ABDC是平行四边形;
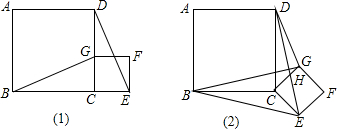
(2)解:作FG⊥DC交DC延长线于G,如图所示: 则∠DGF=90°,
则∠DGF=90°,
∵∠CDF=45°,
∴△FDG是等腰直角三角形,
∴FG=DG,
∵FB=8,
∴CD=AB=$\frac{1}{2}$FB=4,
设CG为x,则FG=DG=4+x,
在Rt△CFG中,根据勾股定理得:FG2+CG2=CF2,
即(4+x)2+x2=($\sqrt{26}$)2,
解得:x=1,或x=-5(舍去),
∴x=1,
∴FG=5,
∴△CDF的面积=$\frac{1}{2}$CD•FG=$\frac{1}{2}$×4×5=10.
点评 本题考查了平行四边形的判定、三角形中位线定理、等腰直角三角形的判定与性质以及勾股定理、三角形面积的计算;本题有一定难度,特别是(2)中,需要通过作辅助线,设未知数列出方程才能求出结果.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连接CF.
已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/件) | 100 | 105 | 110 | 115 | 120 |
| 销量y(件) | 60 | 50 | 40 | 30 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
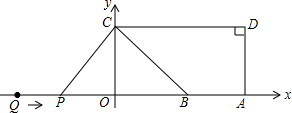 如图,A(5,0),B(3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(-4,0)出发,沿x轴向右以每秒2个单位长度的速度运动,运动时间t秒.
如图,A(5,0),B(3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(-4,0)出发,沿x轴向右以每秒2个单位长度的速度运动,运动时间t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠ABC=90°,∠ABE是等边三角形,点P为射线BC上一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.
如图,已知∠ABC=90°,∠ABE是等边三角形,点P为射线BC上一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com