
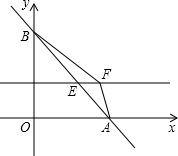
 如图,已知直线y=-$\frac{6}{5}$x+6与x轴交于点A,与y轴交于点B,直线l∥x轴且在一象限交AB于E,F为l上一点,连接AF、BF,线段BF所在的直线y=-x+6.
如图,已知直线y=-$\frac{6}{5}$x+6与x轴交于点A,与y轴交于点B,直线l∥x轴且在一象限交AB于E,F为l上一点,连接AF、BF,线段BF所在的直线y=-x+6.分析 先设出直线l的解析式,表示出点E,F坐标;
(1)由m=2代入点E,F坐标即可得出结论;
(2)用面积公式表示出三角形ABF和四边形AOBF的面积,用面积关系建立方程求解即可;
(3)先确定出直线AM解析式,同(2)的方法分两种情况计算即可.
解答 解:∵直线y=-$\frac{6}{5}$x+6与x轴交于点A,与y轴交于点B,
∴A(0,6),B(5,0),
设直线l的解析式为y=m,(0<m<6),
∵直线l∥x轴且在一象限交AB于E,
∴令y=m,
∴m=-$\frac{6}{5}$x+6.
∴x=$\frac{5}{6}$(6-m),
∴E($\frac{5}{6}$(6-m),m)
∵线段BF所在的直线y=-x+6,
令y=m,
∴-x+6=m,
∴x=6-m,
∴F(6-m,m),
∴G(0,m)
(1)如图1,
∵直线l经过(0,2),
∴E($\frac{10}{3}$,2),F(4,2),
(2)S△ABF=S△BEF+S△AEF=$\frac{1}{2}$EF×BG+$\frac{1}{2}$EF×OG=$\frac{1}{2}$EF×(BG+OG)=$\frac{1}{2}$EF×OB=$\frac{1}{2}$×6[6-m-$\frac{5}{6}$(6-m)]=$\frac{1}{2}$(6-m),
S四边形AOBF=S△BGF+S梯形AOGF=$\frac{1}{2}$FG×BG+$\frac{1}{2}$(GF+OA)×OG=$\frac{1}{2}$(6-m)(6-m)+$\frac{1}{2}$(6-m+5)×m=$\frac{1}{2}$(36-m),
∵△ABF的面积是四边形AOBF面积的$\frac{1}{10}$,
∴$\frac{1}{2}$(6-m)=$\frac{1}{2}$(36-m)×$\frac{1}{10}$,m\
∴m=$\frac{8}{3}$,
∴E($\frac{25}{9}$,$\frac{8}{3}$),F($\frac{10}{3}$,$\frac{8}{3}$),
(3)如图2,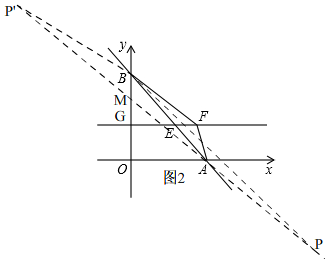
∵M在y轴正半轴上,OM=$\frac{5}{6}$OB=$\frac{5}{6}$×6=5,
∴M(0,5),
∵A(5,0),
∴直线AM解析式为y=-x+5
∵A(5,0),B(0,6),
∴S△AOB=$\frac{1}{2}$OA×OB=15,
∵S△ABP=S△AOB,
∴S△ABP=15,
设P(n,-n+5)
∵点M在OB上,
∴点P只能在线段AM的延长线上或在线段MA的延长线上,
①当点P在AM的延长线上时,S△ABP'=S△BMP'+S△BMA=$\frac{1}{2}$BM×|xP|+$\frac{1}{2}$BM×|xA|=$\frac{1}{2}$BM×(|xP|+|xA|)=$\frac{1}{2}$×1×(|n|+5)=15,
∴n=25(舍)或n=-25,
∴P'(-25,30),
当点P在MA的延长线上时,S△ABP=S△BMP-S△BMA=$\frac{1}{2}$BM×|xP|-$\frac{1}{2}$BM×|xA|=$\frac{1}{2}$BM×(|xP|-|xA|)=$\frac{1}{2}$×1×(|n|-5)=15,
∴n=-35(舍)或n=35,
∴P'(35,-30),
故点P的坐标(-25,30)或(35,-30).
点评 此题是一次函数综合题,主要考查了待定系数法,三角形,梯形的面积公式,解本题的关键是坐标系中几何图形的面积的计算方法,是一道比较简单的中考常考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:单选题
若把多项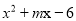 因式后含有因式
因式后含有因式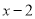 ,则
,则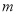 为( )
为( )
A. -1 B. 1 C. 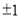 D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
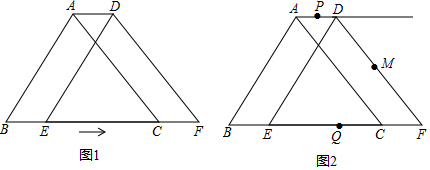
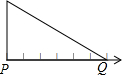 慧慧自己做了一个三角形的纸板,并在其中一边画了七个等距离的小黑点,每相邻两个小黑点之间的距离为1个单位长度,现把此边放在如图所示的数轴上,若点P所表示的数是-1.6,则点Q所表示的数是4.4.
慧慧自己做了一个三角形的纸板,并在其中一边画了七个等距离的小黑点,每相邻两个小黑点之间的距离为1个单位长度,现把此边放在如图所示的数轴上,若点P所表示的数是-1.6,则点Q所表示的数是4.4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
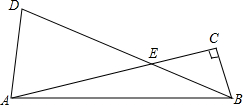 在Rt△ABC中,∠CAB=α,斜边AB绕点B顺时针旋转2α角度得到DB,交AC于点E,连接AD,记AD=kBE.
在Rt△ABC中,∠CAB=α,斜边AB绕点B顺时针旋转2α角度得到DB,交AC于点E,连接AD,记AD=kBE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com