
【题目】某果园的工人需要摘苹果园和梨园的果实,苹果园的果实是梨园的![]() 倍,如果前三天工人都在苹果园摘果实,第四天,
倍,如果前三天工人都在苹果园摘果实,第四天,![]() 的工人到梨园摘果实,剩下
的工人到梨园摘果实,剩下![]() 的工人仍在苹果园摘果实,则第四天结束后苹果园的果实全部摘完,梨园剩下的果实正好是
的工人仍在苹果园摘果实,则第四天结束后苹果园的果实全部摘完,梨园剩下的果实正好是![]() 名工人
名工人![]() 天的工作量.如果前三天工人都在苹果园摘果实,要使苹果和梨同时摘完,则第四天开始,再外请一个工人的情况下,应该安排___人摘苹果.(假定工人们每人每天摘果实的数量是相等的,且每人每天的工作时间相等)
天的工作量.如果前三天工人都在苹果园摘果实,要使苹果和梨同时摘完,则第四天开始,再外请一个工人的情况下,应该安排___人摘苹果.(假定工人们每人每天摘果实的数量是相等的,且每人每天的工作时间相等)
【答案】![]()
【解析】
本题根据工人的安排和完成时间,可以用关于人数的未知数表示出来工作总量,根据工作总量的倍数关系求出人数,即可求出答案.
解:假设工人一共有3a人,每人每天的工作量为1份,
则苹果园工作总量:3a×3+3a×![]() =10a
=10a
梨园工作总量:3a×![]() +4×2=2a+8
+4×2=2a+8
由苹果园的工作量是梨园的4倍可知:
10a=(2a+8)×4
解得:a=16
所以共有工人16×3=48(人)
苹果园工作量:10a=10×16=160(份)
梨园工作量:2a+8=2×16+8=40(份)
前三天工人全部在苹果园,可以完成工作:48×3=144(份)
还剩下工作:160-144=16(份)
苹果园剩下的工作要和梨园同时完成,故工人应该按照工作量来分配,
苹果园需要安排工人(48+1)×![]() (人)
(人)
故答案为:14.


科目:初中数学 来源: 题型:
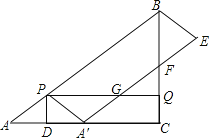
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作A′PBE,A′E交射线BC于点F,交射线PQ于点G.设A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
(1)当t为何值时,点A′与点C重合;
(2)用含t的代数式表示QF的长;
(3)求S与t的函数关系式;
(4)请直接写出当射线PQ将A′PBE分成的两部分图形的面积之比是1:3时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
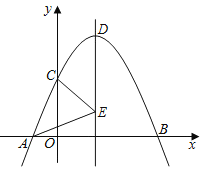
【题目】如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(﹣1,0)、B(5,0),与y轴相交于点C(0,![]() ).
).
(1)求该函数的表达式;
(2)设E为对称轴上一点,连接AE、CE;
①当AE+CE取得最小值时,点E的坐标为 ;
②点P从点A出发,先以1个单位长度/的速度沿线段AE到达点E,再以2个单位长度的速度沿对称轴到达顶点D.当点P到达顶点D所用时间最短时,求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=12,半径OC⊥AB,D为弧BC上一动点(不包括B、C两点),DE⊥OC,DF⊥AB,垂足分别为E.F.
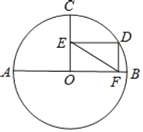
(1)求EF的长.
(2)若点E为OC的中点,
①求弧CD的度数.
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开州区厚坝镇大力发展经济作物,其中果树种植已初具规模,今年受气候、雨水等因素的影响,櫻桃较去年有小幅度的减产,而枇杷有所增产.
(1)该镇某果农今年收获櫻桃和枇杷共![]() 千克,其中枇杷的产量不超过樱桃产量的
千克,其中枇杷的产量不超过樱桃产量的![]() 倍,求该果农今年收获樱桃至少多少千克?
倍,求该果农今年收获樱桃至少多少千克?
(2)该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售,该果农去年櫻桃的市场销售量为![]() 千克,销售均价为
千克,销售均价为![]() 元千克,今年樱桃的市场销售量比去年减少了
元千克,今年樱桃的市场销售量比去年减少了![]() ,销售均价比去年增加
,销售均价比去年增加![]() ,该果农去年枇杷的市场销售量为
,该果农去年枇杷的市场销售量为![]() 千克,销售均价为
千克,销售均价为![]() 元千克,今年枇杷的市场销售量比去年增加了
元千克,今年枇杷的市场销售量比去年增加了![]() ,但销售均价比去年减少了
,但销售均价比去年减少了![]() ,该果农今年运往市场销售的这部分櫻桃和枇杷的销售总金额与他去年櫻桃和枇杷的市场销售总金额相同.求
,该果农今年运往市场销售的这部分櫻桃和枇杷的销售总金额与他去年櫻桃和枇杷的市场销售总金额相同.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
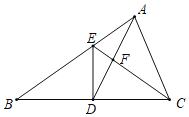
【题目】如图,在△ABC中,AD是BC边上的中线,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)过点A作AM⊥BC于点M,求DE:AM的值;
(3)若S△FCD=5,BC=10,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店某种文具进价为每件20元,市场调查反映:当售价为每件30元时,平均每星期可售出140件;而昂每件售价涨1元,平均每星期少售出10件,设每件涨价![]() 元,平均每星期的总利润为
元,平均每星期的总利润为![]() 元.
元.
(1)写出![]() 与
与![]() 的函数关系式,并求出自变量的取值范围;
的函数关系式,并求出自变量的取值范围;
(2)如何定价才能使每星期的利润最大?且每星期的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
阅读理解:数学兴趣小组在探究如何求![]() 的值,经过思考、讨论、交流,得到以下思路:
的值,经过思考、讨论、交流,得到以下思路:
如图1,作![]() ,使
,使![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.![]()
![]() .
.
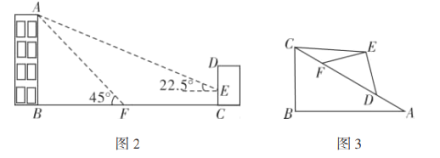
请解决下列问题:
(1)类比求解:求出![]() 的值;
的值;
(2)问题解决:如图2,某住宅楼![]() 的后面有一建筑物
的后面有一建筑物![]() ,当光线与地面的夹角是
,当光线与地面的夹角是![]() 时,住宅在建筑物的墙上留下高
时,住宅在建筑物的墙上留下高![]() 的影子
的影子![]() ;而当光线与地面的夹角是
;而当光线与地面的夹角是![]() 时,住宅楼顶
时,住宅楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有
有![]() 的距离(
的距离(![]() ,
,![]() ,
,![]() 在一条直线上).求住宅楼
在一条直线上).求住宅楼![]() 的高度(结果保留根号);
的高度(结果保留根号);
(3)探究发现:如图3,小明用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .他将
.他将![]() 的斜边
的斜边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() ,
,![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).探究在
重合).探究在![]() 移动过程中,是否存在某个位置,使得
移动过程中,是否存在某个位置,使得![]() ?如果存在,直接写出
?如果存在,直接写出![]() 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com