
分析 先算括号里面的,再算除法,最后把x=$\frac{7}{2}$与x=$\frac{1}{2}$代入进行计算即可.
解答 解:原式=[$\frac{x+1-x}{x}$]•$\frac{x-4}{(x-4)^{2}}$
=$\frac{1}{x}$•$\frac{1}{x-4}$
=$\frac{1}{x(x-4)}$,
当x=$\frac{7}{2}$时,原式=$\frac{1}{\frac{7}{2}×(\frac{7}{2}-4)}$=-$\frac{4}{7}$;
当x=$\frac{1}{2}$时,原式=$\frac{1}{\frac{1}{2}×(\frac{1}{2}-4)}$=-$\frac{4}{7}$,
∴她的计算结果也是正确的.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
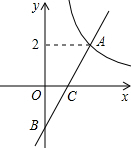 已知,在平面直角坐标系xOy中,函数y=$\frac{4}{x}$(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).
已知,在平面直角坐标系xOy中,函数y=$\frac{4}{x}$(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
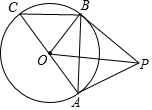 如图,已知AC是⊙O的直径,BC是⊙O的弦,P是⊙O外一点,连接PB,AB,OB,且∠PBA=∠ACB.
如图,已知AC是⊙O的直径,BC是⊙O的弦,P是⊙O外一点,连接PB,AB,OB,且∠PBA=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于A、B、C,直线DF分别交l1、l2、l3于D、E、F,AC交DF于H,若AH=2,HB=1,BC=5,则$\frac{DE}{EF}$的值为$\frac{3}{5}$,$\frac{DH}{HF}$的值为$\frac{1}{3}$.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于A、B、C,直线DF分别交l1、l2、l3于D、E、F,AC交DF于H,若AH=2,HB=1,BC=5,则$\frac{DE}{EF}$的值为$\frac{3}{5}$,$\frac{DH}{HF}$的值为$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com