
 如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:
如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:分析 利用大正方形的边长=长方形的长+长方形的宽,小正方形的边长=长方形的长-长方形的宽,大正方形的面积-小正方形的面积=4个长方形的面积,完全平方公式x2+y2=(x+y)2-2xy,进而判定即可.
解答 解:由图形可得:①大正方形的边长=长方形的长+长方形的宽,故x+y=a正确;
②小正方形的边长=长方形的长-长方形的宽,故x-y=b正确;
③大正方形的面积-小正方形的面积=4个长方形的面积,故a2-b2=4xy错误;
④根据①知x+y=a,根据②知x-y=b,则x2-y2=ab,正确;
⑤x2+y2=(x+y)2-2xy=a2-2×$\frac{{a}^{2}-{b}^{2}}{4}$=$\frac{{a}^{2}+{b}^{2}}{2}$,正确.
所以正确的是①②④⑤.
故答案为:①②④⑤.
点评 本题考查了图形的面积、整式的混合运算以及因式分解的应用,主要考查学生的计算能力和观察图形的能力.


科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.点Q在直线AB上,点P在x轴上,且∠OQP=90°.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.点Q在直线AB上,点P在x轴上,且∠OQP=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2,3 | B. | 1,1,$\sqrt{2}$ | C. | 1,1,$\sqrt{3}$ | D. | 1,2,$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将n个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5,…是正方形对角线的交点,那么阴影部分面积之和等于$\frac{1}{4}$(n-1).
将n个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5,…是正方形对角线的交点,那么阴影部分面积之和等于$\frac{1}{4}$(n-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
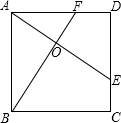 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AO=OE (2)S△AOB=S四边形DEOF (3)AE=BF (4)AE⊥BF中,正确的有(2)、(3)、(4)..
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AO=OE (2)S△AOB=S四边形DEOF (3)AE=BF (4)AE⊥BF中,正确的有(2)、(3)、(4)..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com