
【题目】如图,在![]() 中,
中,![]() ,高
,高![]() 、
、![]() 相交于点
相交于点![]() ,
, ![]() ,且
,且![]() .
.
(1)求线段 ![]() 的长;
的长;
(2)动点 ![]() 从点
从点 ![]() 出发,沿线段
出发,沿线段 ![]() 以每秒 1 个单位长度的速度向终点
以每秒 1 个单位长度的速度向终点 ![]() 运动,动点
运动,动点 ![]() 从 点
从 点 ![]() 出发沿射线
出发沿射线![]() 以每秒 4 个单位长度的速度运动,
以每秒 4 个单位长度的速度运动,![]() 两点同时出发,当点
两点同时出发,当点 ![]() 到达
到达 ![]() 点时,
点时,![]() 两点同时停止运动.设点
两点同时停止运动.设点 ![]() 的运动时间为
的运动时间为 ![]() 秒,
秒,![]() 的面积为
的面积为 ![]() ,请用含
,请用含![]() 的式子表示
的式子表示 ![]() ,并直接写出相应的
,并直接写出相应的 ![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点 ![]() 是直线
是直线![]() 上的一点且
上的一点且 ![]() .是否存在
.是否存在![]() 值,使以点
值,使以点 ![]() 为顶 点的三角形与以点
为顶 点的三角形与以点 ![]() 为顶点的三角形全等?若存在,请直接写出符合条件的
为顶点的三角形全等?若存在,请直接写出符合条件的 ![]() 值; 若不存在,请说明理由.
值; 若不存在,请说明理由.

【答案】(1)5;(2)①当点![]() 在线段
在线段![]() 上时,
上时,![]() ,
,![]() 的取值范围是
的取值范围是![]() ;②当点
;②当点![]() 在射线
在射线![]() 上时,
上时,![]() ,,
,,![]() 的取值范围是
的取值范围是![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)只要证明△AOE≌△BCE即可解决问题;
(2)分两种情形讨论求解即可①当点Q在线段BD上时,QD=2-4t,②当点Q在射线DC上时,DQ=4t-2时;
(3)分两种情形求解即可①如图2中,当OP=CQ时,BOP≌△FCQ.②如图3中,当OP=CQ时,△BOP≌△FCQ;
解:(1)∵![]() 是高,∴
是高,∴![]()
∵![]() 是高,∴
是高,∴![]()
∴![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中,
中,
∴![]() ≌
≌![]()
∴![]() ;
;
(2)∵![]() ,
,![]()
∴![]() ,
,![]() ,
,
根据题意,![]() ,
,![]() ,
,
①当点![]() 在线段
在线段![]() 上时,
上时,![]() ,
,
∴![]() ,
,![]() 的取值范围是
的取值范围是![]() .
.
②当点![]() 在射线
在射线![]() 上时,
上时,![]() ,
,
∴![]() ,
,![]() 的取值范围是
的取值范围是![]()
(3)存在.
①如图2中,当OP=CQ时,∵OB=CF,∠POB=∠FCQ,∴△BOP≌△FCQ.
∴CQ=OP,
∴5-4t═t,
解得t=1,
②如图3中,当OP=CQ时,∵OB=CF,∠POB=∠FCQ,∴△BOP≌△FCQ.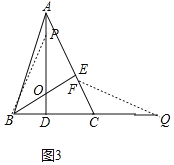
∴CQ=OP,
∴4t-5=t,
解得t=![]() .
.
综上所述,t=1或![]() s时,△BOP与△FCQ全等.
s时,△BOP与△FCQ全等.


科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,对角线AC、BD交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°.
(1)求证:△AOB是等边三角形;
(2)求∠BOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时 间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
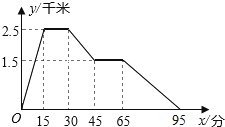
A. 体育场离张强家2.5千米
B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店1.千米
D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
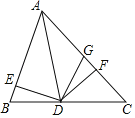
【题目】如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com