
【题目】图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图b的形状拼成一个正方形. 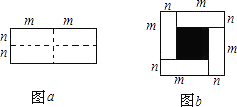
(1)你认为图b中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图b中阴影部分的面积. 方法1:(只列式,不化简)
方法2:(只列式,不化简)
(3)观察图b你能写出下列三个代数式之间的等式关系吗? 代数式:(m+n)2 , (m﹣n)2 , mn.
(4)根据(2)题中的等量关系,解决如下问题: 若a+b=8,ab=5.求(a﹣b)2 .
【答案】
(1)m﹣n
(2)边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积, 即(m﹣n)2=(m+n)2﹣4mn;边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,即(m﹣n)2=(m+n)2﹣2m×2n
(3)(m+n)2=(m﹣n)2+4mn
(4)解:∵a+b=8,ab=5,
∴(a+b)2=64,
∴(a﹣b)2+4ab=64,
∴(a﹣b)2=64﹣4×5=44
【解析】解:(1)阴影部分的正方形边长是:m﹣n. 所以答案是:m﹣n;(2)阴影部分的面积就等于边长为m﹣n的小正方形的面积,
方法1:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,
即(m﹣n)2=(m+n)2﹣4mn;方法2:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,即(m﹣n)2=(m+n)2﹣2m×2n;(3)由题意可得:(m+n)2=(m﹣n)2+4mn.所以答案是:(m+n)2=(m﹣n)2+4mn.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】对于函数 y=﹣3x+1,下列结论正确的是( )
A. 它的图象必经过点(﹣1,3) B. 它的图象经过第一、二、三象限
C. y的值随x值的增大而增大 D. 当x>1时,y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用●表示实心圆,用○表示空心圆,现有若干个实心圆与空心圆,按一定的规律排列如下:●○●●○●●●○●○●●○●●●○●○●●○●●●○…问:前2016个圆中,有个空心圆.
查看答案和解析>>
科目:初中数学 来源: 题型:
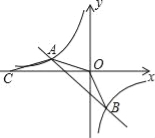
【题目】如图,直线AB与反比例函数的图象交于A(﹣4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.
(1)求反比例函数的解析式.
(2)求cos∠OBA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=![]() 或
或![]() .
.
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
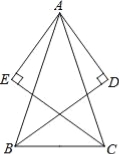
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC,CE平分∠ACB,过点A分别作BD、CE的垂线段AD、AE,垂足为D、E,求证:AD=AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③b2+8a>4ac;④abc>0,其中正确的有( ).
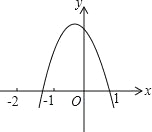
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com