
����Ŀ����ͼ������ABCD�У�P�DZ�AD�ϵ�һ���㣬����BP��CP������B�����߽��߶�CP���ӳ����ڵ�E����AD���ڵ�M����ʹ����ABE=��CBP�����AB=2��BC=5��AP=x��PM=y.
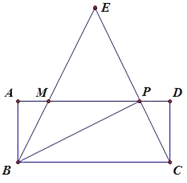
��1��˵����ABM�ס�APB�������y����x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
��2����AP=4ʱ����sin��EBP��ֵ��
��3�������EBC������EBCΪ�ǵĵ��������Σ���AP�ij���
���𰸡���1��֤����������y=x��![]() ��2��x��5����2��
��2��x��5����2��![]() ����3��4��
����3��4��![]() ��
��
��������
��1����֤��ABM�ס�APB��Ȼ��������������ε����ʾͿɵõ�y����x�ĺ�������ʽ����P�DZ�AD�ϵ�һ����ɵ�0��x��5������y��0�Ϳ�����ú������Ա���ȡֵ��Χ��
��2������M��MH��BP��H����AP=x=4�����MP��AM��BM��BP��Ȼ���������������MH���Ӷ������BH���Ϳ������EBP������ֵ��
��3���ɷ�EB=EC��CB=CE����������ۣ�����EB=ECʱ����֤����AMB�ա�DPC������AM=DP���Ӷ���x-y=5-x����y=2x-5�����루1���к�������ʽ�Ϳ����x��ֵ������CB=CEʱ���ɵõ�PC=EC-EP=BC-MP=5-y����Rt��DPC�и��ݹ��ɶ����ɵõ�x��y�Ĺ�ϵ��Ȼ����y����x�ĺ�������ʽ���Ϳ����x��ֵ��
�⣺��1�����ı���ABCD�Ǿ���
��AD��BC
���CBP=��BPA
�ߡ�ABE=��CBP��
����A=��A��
���ABM�ס�APB
����ABM�ס�APB����![]() ��
��
��![]() ��
��
��y=x��![]() ��
��
��P�DZ�AD�ϵ�һ���㣬
��0��x��5��
��y��0��
��x��![]() ��0��
��0��
��x��2��
��x��ȡֵ��ΧΪ2��x��5��
��2������M��MH��BP��H����ͼ��
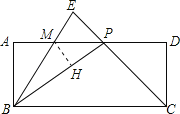
��AP=x=4����y=x��![]() =3��
=3��
��MP=3��AM=1��
��BM=![]() ��BP=
��BP=![]() ��
��
��S��BMP=![]() MPAB=
MPAB=![]() BPMH��
BPMH��
��MH=![]() ��
��
��sin��EBP=![]() ��
��
��3������EB=EC��������EBC=��ECB��
��֤��AMB�ա�DPC��
��AM=DP��
��x��y=5��x��
��y=2x��5��
��x��![]() =2x��5��
=2x��5��
��ã�x1=1��x2=4��
��2��x��5��
��AP=x=4��
����CE=CB������EBC=��E��
��AD��BC��
���EMP=��EBC=��E��
��PE=PM=y��
��PC=EC��EP=5��y��
����Rt��DPC����5��y��2����5��x��2=22��
��3x2��10x��4=0��
��ã�x1=![]() ��x2=
��x2=![]() ����ȥ����
����ȥ����
��AP=x=![]() ��
��
����������AP��ֵΪ4��![]() ��
��


 �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д� ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ��
��![]() ��ֱ��
��ֱ��![]() �ӳ����ϣ���
�ӳ����ϣ���![]() Ϊ
Ϊ![]() �ϣ���
�ϣ���![]() ��
��![]() ����
����![]() ���ӳ����ཻ��
���ӳ����ཻ��![]() ��
��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�![]() ��
��![]() ��
��
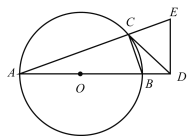
��1����֤��![]() ��
��
��2����![]() �ij���
�ij���
��3����![]() ��ƽ������
��ƽ������![]() ���ڵ�
���ڵ�![]() ��
��![]() Ϊ
Ϊ![]() �����ģ���
�����ģ���![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱�ս������������ѧʵ��������ԣ�ijУ�Գ���ѧ��������ģ��ѵ������������ѧ����3����ͬ�IJ���ʵ����Ŀ��������Ŀ����Ţ١��ڡ��۱�ʾ����ѧ��Ŀ����ĸa��b��c��ʾ������ʱÿ��ѧ��ÿ��ֻ����һ��ʵ�飬ʵ�����Ŀ��ѧ����ǩȷ������һ�γ�ǩȷ������ʵ����Ŀ���ڶ��γ�ǩȷ����ѧʵ����Ŀ��
��1��С��ͬѧ�鵽����ʵ����Ŀ������һ���� �¼���������Ȼ���������������������������
��2��С��ͬѧ�������Ģ١��ںͻ�ѧ��c��ʵ�����ýϺã����û�����ͼ�����б����ķ���������ͬʱ�鵽���ƶ����ýϺõ�ʵ����Ŀ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx��3��x�ύ��A��B���㣬��y�ύ�ڵ�C����OB��OC��3OA���������ߵĽ���ʽ��������
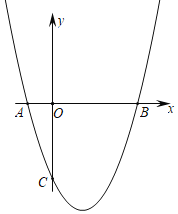
A.y��x2��2x��3B.y��x2��2x+3C.y��x2��2x��4D.y��x2��2x��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪԭ�㣬��O�İ뾶Ϊ1����A������Ϊ��2��0��������B����O�ϣ���ABΪ�����ȱߡ�ABC��˳ʱ�룩�����߶�OC����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x+6��x�ᡢy��ֱ���A��B���㣬��ֱ��l1����y��������ƽ��һ�ξ���õ�ֱ��l2��y���ڵ�M����l1��l2֮��ľ���Ϊ3����C��x��y����ֱ��11�ϵ�һ�����㣬����C��AB�Ĵ���CD��y���ڵ�D��
x+6��x�ᡢy��ֱ���A��B���㣬��ֱ��l1����y��������ƽ��һ�ξ���õ�ֱ��l2��y���ڵ�M����l1��l2֮��ľ���Ϊ3����C��x��y����ֱ��11�ϵ�һ�����㣬����C��AB�Ĵ���CD��y���ڵ�D��

��1����ֱ��l2�Ľ���ʽ��
��2����C�˶���ʲôλ��ʱ����AOD�����Ϊ21![]() �������ʱ��C�����ꣻ
�������ʱ��C�����ꣻ
��3������AM������ABM���ŵ�M��ת�õ���A'B'M'����ƽ�����Ƿ����һ��N��ʹ�ı���AMA'NΪ���Σ������ڣ������N�����꣺�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
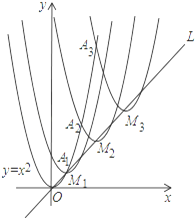
����Ŀ����ͼ��������y��x2�ڵ�һ�����ھ����������㣨�����꣬�����궼Ϊ�����ĵ㣩����ΪA1��A2��A3����An��������������y��x2��ֱ��L��y��x����ƽ�ƣ���һϵ�������ߣ�����������������
�������ߵĶ���M1��M2��M3����Mn��������ֱ��L��y��x�ϣ�
���������������A1��A2��A3��An������
��M2016���������Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
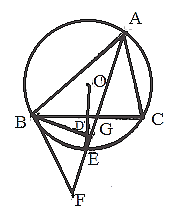
����Ŀ����ͼ����EΪ��ABC�����Բ��O��һ�㣬OE��BC�ڵ�D������AE���ӳ�����F��ʹ��FBC����BAC��
��1����֤��ֱ��BF�ǡ�O�����ߣ�
��2������DΪOE�е㣬����B��BG��AF�ڵ�G������DG����O�İ뾶Ϊ![]() ,AC=5.
,AC=5.
�����BAC�Ķ�����
�����߶�DG�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OAB��O����ʱ����ת60��õ���OCD����OA��4����AOB��35�㣬�����н��۴�����ǣ�������
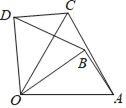
A. ��BDO��60�� B. ��BOC��25�� C. OC��4 D. BD��4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com