
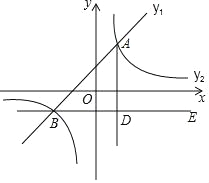
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象交于点A(1,2)和B(﹣2,m).
的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1≥y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若∠DAC=30°,求点C的坐标.
【答案】(1)反比例函数的解析式为y2=![]() ;一次函数解析式为y1=x+1.(2)当﹣2≤x<0或x≥1时,y1≥y2.(3)点C的坐标为(1﹣
;一次函数解析式为y1=x+1.(2)当﹣2≤x<0或x≥1时,y1≥y2.(3)点C的坐标为(1﹣![]() ,﹣1)或(1+
,﹣1)或(1+![]() ,﹣1).
,﹣1).
【解析】
(1)由点A的坐标,利用反比例函数图象上点的坐标特征可求出k值,由点B的横坐标利用反比例函数图象上点的坐标特征可求出m值,进而可得出点B的坐标,根据点A,B的坐标,利用待定系数法即可求出一次函数解析式;
(2)观察函数图象,由两函数图象的上下位置关系结合两交点的坐标,即可找出y1≥y2时x的取值范围;
(3)由点A,B的纵坐标可得出AD的长度及点D的坐标,在Rt△ADC中,由∠DAC=30°可得出CD的长度,再结合点D的坐标即可求出点C的坐标.
(1)∵点A(1,2)在反比例函数y2=![]() 的图象上,
的图象上,
∴2=![]() ,
,
∴k=1×2=2,
∴反比例函数的解析式为y2=![]() .
.
∵点B(﹣2,m)在反比例函数y2=![]() 的图象上,
的图象上,
∴m=![]() =﹣1,
=﹣1,
∴点B的坐标为(﹣2,﹣1).
把A(1,2),B(﹣2,﹣1)代入y1=ax+b得:![]()
解得:![]()
∴一次函数解析式为y1=x+1.
(2)由函数图象可知:当﹣2≤x<0或x≥1时,y1≥y2.
(3)由题意得:AD=2﹣(﹣1)=3,点D的坐标为(1,﹣1).
在Rt△ADC中,tan∠DAC=![]() ,即
,即![]() ,
,
解得:CD=![]() .
.
当点C在点D的左侧时,点C的坐标为(1﹣![]() ,﹣1);
,﹣1);
当点C在点D的右侧时,点C的坐标为(1+![]() ,﹣1).
,﹣1).
∴点C的坐标为(1﹣![]() ,﹣1)或(1+
,﹣1)或(1+![]() ,﹣1).
,﹣1).


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
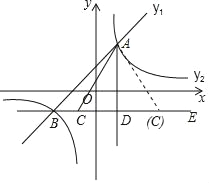
【题目】已知:AD是△ABC的高,且BD=CD.
(1)如图1,求证:∠BAD=∠CAD;
(2)如图2,点E在AD上,连接BE,将△ABE沿BE折叠得到△A′BE,A′B与AC相交于点F,若BE=BC,求∠BFC的大小;
(3)如图3,在(2)的条件下,连接EF,过点C作CG⊥EF,交EF的延长线于点G,若BF=10,EG=6,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
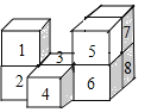
【题目】如图,是用8个大小相同的小正方体搭成的几何体,仅在该几何体中取走一块小正方体,使得到的新几何体同时满足两个要求:(1)从正面看到的形状和原几何体从正面看到的形状相同;(2)从左面看到的形状和原几何体从左面看到的形状也相同.在不改变其它小正方体位置的前提下,可取走的小正方体的标号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC中,∠ACB=90°,CA=CB,点D,E分别在CB,CA上,且CD=CE,连AD,BE,F为AD的中点,连CF.
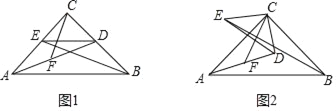
(1)求证:CF=![]() BE,且CF⊥BE;
BE,且CF⊥BE;
(2)将△CDE绕点C顺时针旋转一个锐角(如图2),其它条件不变,此时(1)中的结论是否仍成立?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
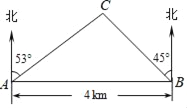
【题目】如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东53°方向上,从B测得灯塔C在北偏西45°方向上,求灯塔C与观测点A的距离(精确到0.1km).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
(1)请按要求对△ABO作如下变换:
①将△OAB向下平移2个单位,再向左平移3个单位得到△O1A1B1;
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA2B2.
(2)写出点A1,A2的坐标: , ;
(3)△OA2B2的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
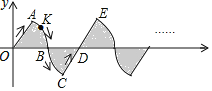
【题目】在平面直角坐标系xOy中,若干个半径为1个单位长度,圆心角是![]() 的扇形按图中的方式摆放,动点K从原点O出发,沿着“半径OA
的扇形按图中的方式摆放,动点K从原点O出发,沿着“半径OA![]() 弧AB
弧AB![]() 弧BC
弧BC![]() 半径CD
半径CD![]() 半径DE
半径DE![]() ”的曲线运动,若点K在线段上运动的速度为每秒1个单位长度,在弧线上运动的速度为每秒
”的曲线运动,若点K在线段上运动的速度为每秒1个单位长度,在弧线上运动的速度为每秒![]() 个单位长度,设第n秒运动到点K,
个单位长度,设第n秒运动到点K,![]() 为自然数
为自然数![]() ,则
,则![]() 的坐标是____,
的坐标是____,![]() 的坐标是____
的坐标是____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com