
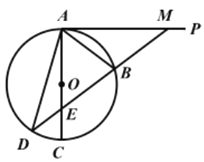
【题目】如图,AC是⊙O的一条弦,AP是⊙O的切线。作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=5,AB=6,求AD的长.
【答案】(1)见解析;(2) AD=![]() 。
。
【解析】
(1)由切线的性质可得∠BAE+∠MAB=90°,进而得∠AEB+∠AMB=90°,由等腰三角形的性质得∠MAB=∠AMB,继而得到∠BAE=∠AEB,根据等角对等边即可得结论;
(2)连接BC,根据直径所对的圆周角是直角可得∠ABC=90°,利用勾股定理可求得BC=8,证明△ABC∽△EAM,可得∠C=∠AME,![]() ,可求得AM=
,可求得AM=![]() ,再由圆周角定理以及等量代换可得∠D=∠AMD,继而根据等角对等边即可求得AD=AM=
,再由圆周角定理以及等量代换可得∠D=∠AMD,继而根据等角对等边即可求得AD=AM=![]() .
.
(1)∵AP是⊙O的切线,
∴∠EAM=90°,
∴∠BAE+∠MAB=90°,∠AEB+∠AMB=90°,
又∵AB=BM,
∴∠MAB=∠AMB,
∴∠BAE=∠AEB,
∴AB=BE;
(2)连接BC,
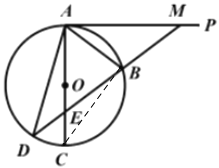
∵AC是⊙O的直径,
∴∠ABC=90°
在Rt△ABC中,AC=10,AB=6,
∴BC=![]() =8,
=8,
由(1)知,∠BAE=∠AEB,
又∠ABC=∠EAM=90°,
∴△ABC∽△EAM,
∴∠C=∠AME,![]() ,
,
即![]() ,
,
∴AM=![]() ,
,
又∵∠D=∠C,
∴∠D=∠AMD,
∴AD=AM=![]() .
.


科目:初中数学 来源: 题型:
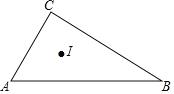
【题目】已知∠ACB=90°,∠CAB=a,且sina=![]() ,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年村该村的人均收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步丰富校园活动,学校准备购买一批足球和篮球,已知购买7个足球和5个篮球的费用相同;购买40个足球和20个篮球共需3400元.
(1)求每个足球和篮球各多少元?
(2)如果学校计划购买足球和篮球共80个,总费用不超过4800元,那么最多能买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )
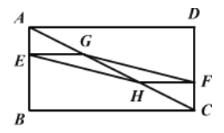
A. 1B. ![]() C. 2D. 4
C. 2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
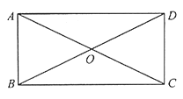
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() ),其对称轴是
),其对称轴是![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() ,
,![]() 之间.有下列结论:①
之间.有下列结论:①![]() ;②
;②![]() ;③若此抛物线过
;③若此抛物线过![]() 和
和![]() 两点,则
两点,则![]() ,其中,正确结论的个数为( )
,其中,正确结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A. B两点,与y轴交于点D(0,6).
+bx+c经过A. B两点,与y轴交于点D(0,6).
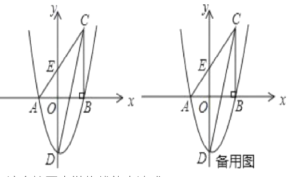
(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com