
【题目】如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°.若∠AOC=40°.
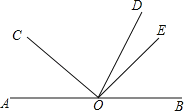
(1)求∠DOE的度数;
(2)图中互为余角的角有 .
【答案】(1)∠DOE=20°;(2)图中互为余角的角有∠AOC和∠BOE,∠COD和∠DOE,∠BOD和∠DOE.
【解析】
(1)利用平角的定义求得∠BOC,然后利用角平分线的性质求得∠COD,再利用余角的定义即可求得结论;
(2)利用角平分线的性质及余角的定义和性质即可找到.
(1)∵∠AOC=40°,
∴∠BOC=180°﹣∠AOC=140°,
∵OD平分∠BOC,
∴∠COD=![]() ∠BOC=70°,
∠BOC=70°,
∵∠COE=90°,
∴∠DOE=90°﹣70°=20°.
(2)∵∠COE=90°,
∴∠AOC+∠BOE=90°,∠COD+∠DOE=90°,
∵OD平分∠BOC,
∴∠COD=∠BOD,
∴∠BOD+∠DOE=90°,
∴图中互为余角的角有∠AOC和∠BOE,∠COD和∠DOE,∠BOD和∠DOE;


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】为鼓励市民节约用水,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费相同.如表是小明家1-4月
用水量和交费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨。
(2)若小明家5月份用水20吨,则应缴水费 元。
(3)若小明家6月份应交水费46元,则6月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
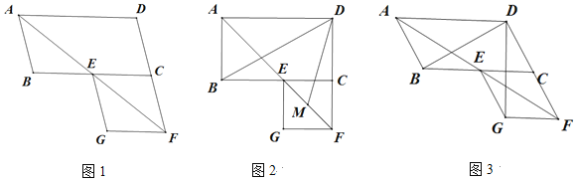
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将8个同样大小的小正方体搭成如图所示的几何体,请按照要求解答下列问题:
(1)从正面、左面、上面观察如图所示的几何体,分别画出所看到的几何体的形状图;
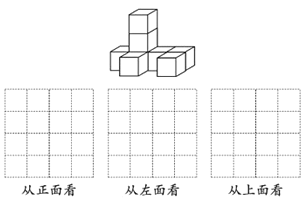
(2)如果在这个几何体上再摆放一个相同的小正方体,并保持这个几何体从上面看和从左面看到的形状图不变.
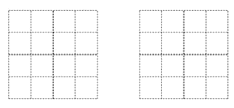
①添加小正方体的方法共有_________种;
②请画出两种添加小正方体后,从正面看到的几何体的形状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
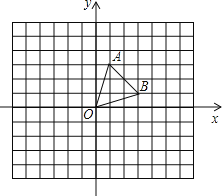
【题目】如图,已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),
(1)请画出把△ABO向下平移5个单位后得到的△A1B1O1的图形;
(2)请画出将△ABO绕点O顺时针旋转90°后得到的△A2B2O2,并写出点A的对应点A2的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以矩形![]() 的顶点
的顶点![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,顶点为点
轴,建立平面直角坐标系,顶点为点![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
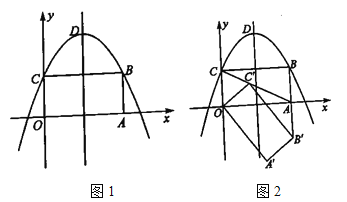
(1)写出抛物线的对称轴及点![]() 的坐标,
的坐标,
(2)将矩形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到矩形
得到矩形![]() .
.
①当点![]() 恰好落在
恰好落在![]() 的延长线上时,如图2,求点
的延长线上时,如图2,求点![]() 的坐标.
的坐标.
②在旋转过程中,直线![]() 与直线
与直线![]() 分别与抛物线的对称轴相交于点
分别与抛物线的对称轴相交于点![]() ,点
,点![]() .若
.若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
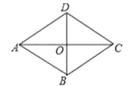
【题目】如图,平行四边形ABCD的两条对角线相交于O,且AC平分∠DAB
(1)求证:四边形ABCD是菱形
(2)若AC=16,BD=12,试求点O到AB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com