
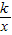 (k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0<m<4)时,点R的坐标是 .(用含m的代数式表示)
(k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0<m<4)时,点R的坐标是 .(用含m的代数式表示)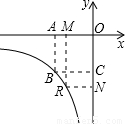
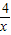 ,所以可以设R的坐标为(x,
,所以可以设R的坐标为(x,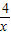 )当R在点B的左边时,S=(-
)当R在点B的左边时,S=(-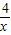 )×(-x-2)=m,由此可以求出x然后求出,那么y;当R在点B右边时,也用同样方法求出x,y.
)×(-x-2)=m,由此可以求出x然后求出,那么y;当R在点B右边时,也用同样方法求出x,y.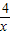 ,
,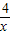 ),
),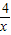 )×(-x-2)=m,
)×(-x-2)=m, ,∴y=
,∴y=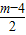 ,
, -2)=m,
-2)=m,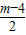 ,∴y=
,∴y=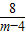 .
. ,
, )或(
)或(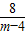 ,
, ).
).

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源:2010年中考数学考前30天冲刺得分专练18:综合测试(解析版) 题型:填空题
 (k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0<m<4)时,点R的坐标是 .(用含m的代数式表示)
(k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0<m<4)时,点R的坐标是 .(用含m的代数式表示)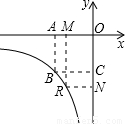
查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前30天冲刺得分专练15:坐标与图形的位置及变换 (解析版) 题型:填空题
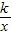 (k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0<m<4)时,点R的坐标是 .(用含m的代数式表示)
(k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0<m<4)时,点R的坐标是 .(用含m的代数式表示)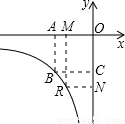
查看答案和解析>>
科目:初中数学 来源:2009年四川省成都市中考数学试卷(解析版) 题型:填空题
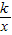 (k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0<m<4)时,点R的坐标是 .(用含m的代数式表示)
(k>0,x<0)的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S,则当S=m(m为常数,且0<m<4)时,点R的坐标是 .(用含m的代数式表示)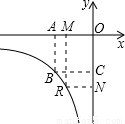
查看答案和解析>>
科目:初中数学 来源:2010年湖北省黄冈市浠水县余堰中学中考数学模拟试卷(解析版) 题型:解答题
 (2009•成都)如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD与⊙O交于点D,与BC交于点E,延长BD,与AC的延长线交于点F,连接CD,G是CD的中点,连接OG.
(2009•成都)如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD与⊙O交于点D,与BC交于点E,延长BD,与AC的延长线交于点F,连接CD,G是CD的中点,连接OG.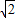 ),求⊙O的面积.
),求⊙O的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com