
 b2=0中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8.则这个三角形的内切圆面积是 .
b2=0中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8.则这个三角形的内切圆面积是 .  b2,利用(x1+x2)2-4x1x2=64可列方程4a2-b2=64;再根据a,b分别是一个面积为12的等腰三角形的腰与底边的长,可得到S△=
b2,利用(x1+x2)2-4x1x2=64可列方程4a2-b2=64;再根据a,b分别是一个面积为12的等腰三角形的腰与底边的长,可得到S△= b×
b× ×
×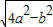 =12,与4a2-b2=64联立方程即可解得b,a的值;再设内切圆半径为x,利用AD2+DF2=AF2=(AE-EF)2,列方程22+x2=(4-x)2,解得半径x,代入三角形的内切圆面积公式即可求解.
=12,与4a2-b2=64联立方程即可解得b,a的值;再设内切圆半径为x,利用AD2+DF2=AF2=(AE-EF)2,列方程22+x2=(4-x)2,解得半径x,代入三角形的内切圆面积公式即可求解.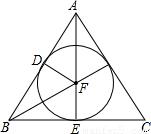 解:如图,AB=AC=a,BC=b,AE⊥BC,FD⊥AB,圆F是△ABC的内切圆,
解:如图,AB=AC=a,BC=b,AE⊥BC,FD⊥AB,圆F是△ABC的内切圆, BC=
BC= b,AE=
b,AE=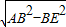 =
=
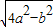 ;
; b2,
b2, b×
b× ×
×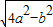 =12,
=12, ;
; )2=
)2=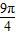 .
.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源:第35章《圆(二)》中考题集(21):35.4 切线的判定(解析版) 题型:填空题
 b2=0中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8.则这个三角形的内切圆面积是 .
b2=0中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8.则这个三角形的内切圆面积是 .查看答案和解析>>
科目:初中数学 来源:第3章《圆》好题集(10):3.5 直线和圆的位置关系(解析版) 题型:填空题
 b2=0中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8.则这个三角形的内切圆面积是 .
b2=0中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8.则这个三角形的内切圆面积是 .查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《一元二次方程》(04)(解析版) 题型:填空题
 b2=0中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8.则这个三角形的内切圆面积是 .
b2=0中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8.则这个三角形的内切圆面积是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com