
| 5 |
| 4 |
| 3 |
| 4 |
| 8 |
| 3 |


科目:初中数学 来源: 题型:
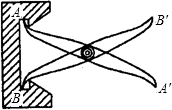 如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?
如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
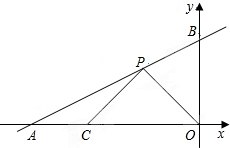 如图,直线AB与x轴、y轴分别交于点A(-6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(-4,0).
如图,直线AB与x轴、y轴分别交于点A(-6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(-4,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com