【题目】.如图，在RT△ABC中，∠C=90°，BC=8，AC=6，动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动，同时点P从A点开始在线段AC上以每秒1个单位长度的速度向点C移动．当一点停止运动，另一点也随之停止运动．设点Q，P移动的时间为t秒．当t=____________ 秒时△APQ与△ABC相似.
科目：初中数学 来源： 题型：
【题目】如图，P是矩形ABCD内一点，连结P与矩形ABCD各顶点，矩形EFGH各顶点分别在边AP，BP，CP，DP上，已知AE＝2EP，EF∥AB，图中两块阴影部分的面积和为S．则矩形ABCD的面积为（ ）
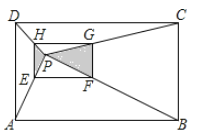
A.4SB.6SC.12SD.18S
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，∠C=45°，sinB=
，AD=1．
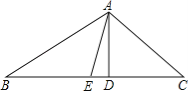
（1）求BC的长；
（2）求tan∠DAE的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，⊙O的直径AB＝12，P是弦BC上一动点（与点B，C不重合），∠ABC＝30°，过点P作PD⊥OP交⊙O于点D．
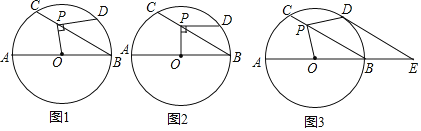
（1）如图2，当PD∥AB时，求PD的长；
（2）如图3，当
时，延长AB至点E，使BE＝
AB，连接DE．
①求证：DE是⊙O的切线；
②求PC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一张透明的平行四边形胶片沿对角线剪开，得到图①中的两张三角形胶片
和
．将这两张三角形胶片的顶点B与顶点E重合，把绕点B顺时针方向旋转，这时AC与DF相交于点O．
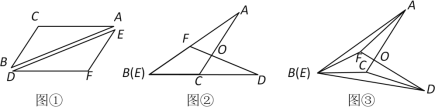
（1）当旋转至如图②位置，点B（E），C,D在同一直线上时，∠AFD与∠DCA的数量关系是 ．
（2）当继续旋转至如图③位置时，（1）中的结论还成立吗？请说明理由．
（3）在图③中，连接BO,AD，探索BO与AD之间有怎样的位置关系，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
的
与
的部分对应值如下表：
| … | -1 | 0 | 1 | 3 | … |
| … | -3 | 1 | 3 | 1 | … |
则下列判断中正确的是（ ）
A.抛物线开口向上B.抛物线与轴的交点在轴负半轴上
C.当
时，
D.方程
的正根在3与4之间
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起，推动了快递行业的高速发展.据调查，岳阳市某家小型快递公司，今年1月份与3月份完成投递的快递总件数分别为8万件和9.68万件.现假定该公司每月投递的快递总件数的增长率相同.
（1）求该快递公司投递快递总件数的月平均增长率.
（2）如果平均每人每月可投递快递0.4万件，那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务？如果不能，请问至少需要增加几名业务员？
查看答案和解析>>
科目：初中数学 来源： 题型：
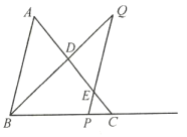
【题目】如图，已知
中，
，
，
，把线段
沿射线
方向平移至
，直线与直线
交于点
，又联结
与直线交于点
.
（1）若
，求
的长；
（2）设
，
，试求
关于
的函数解析式；
（3）当
为多少时，以
、、为顶点的三角形与相似？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据相似多边形的定义，我们把四个角分别相等，四条边成比例的两个凸四边形叫做相似四边形．相似四边形对应边的比叫做相似比．
（1）某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确（直接在横线上填写“真”或“假”）．
①条边成比例的两个凸四边形相似；（ 命题）
②三个角分别相等的两个凸四边形相似；（ 命题）
③两个大小不同的正方形相似．（ 命题）
（2）如图1，在四边形ABCD和四边形A1B1C1D1中，∠ABC＝∠A1B1C1，∠BCD＝∠B1C1D1，
，求证：四边形ABCD与四边形A1B1C1D1相似．
（3）如图2，四边形ABCD中，AB∥CD，AC与BD相交于点O，过点O作EF∥AB分别交AD，BC于点E，F．记四边形ABFE的面积为S1，四边形EFDE的面积为S2，若四边形ABFE与四边形EFCD相似，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
