


 教材全解字词句篇系列答案
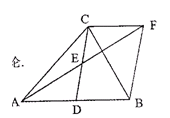
教材全解字词句篇系列答案科目:初中数学 来源:不详 题型:解答题
 的图像交点为A,B。
的图像交点为A,B。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
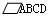 中AD、BC边上的点,AE=CF,
中AD、BC边上的点,AE=CF,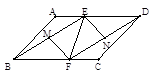
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ②CE=CF ③∠AEB=750 ④BE+DF=EF ⑤
②CE=CF ③∠AEB=750 ④BE+DF=EF ⑤ 其中正确的是 (只填写序号)
其中正确的是 (只填写序号)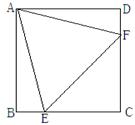
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
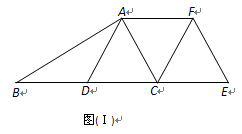
 (0°<
(0°<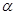 <90°)连结AF、DE.
<90°)连结AF、DE.
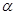 的度数;②当
的度数;②当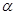 =60°时,请判断四边形ADEF的形状,并给予证明.
=60°时,请判断四边形ADEF的形状,并给予证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com