
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a﹣b+c>0,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣ ![]() ,y2)在该图象上,则y1>y2 , 其中正确的结论是 . (填入正确结论的序号)
,y2)在该图象上,则y1>y2 , 其中正确的结论是 . (填入正确结论的序号) 
【答案】②④
【解析】解:∵抛物线开口向下, ∴a<0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∵对称轴x=﹣ ![]() >0,
>0,
∴b>0,
∴abc<0,故①正确;
∵对称轴x=﹣ ![]() =1,
=1,
∴b=﹣2a,
∴令x=﹣1时,此时y=a﹣b+c,
由图象可知a﹣b+c<0,
∴a+2a+c=3a+c<0,故②正确,③错误;
∵抛物线的对称轴为x=1,
∴﹣1与3关于x=1对称,0与2关于x=1对称,
令x=2时,此时y=4a+2b+c>0,故④正确;
当x<1时,y随着x的增大而增大,
∴﹣2<﹣ ![]() ,
,
∴y1<y2 , 故⑤错误;
所以答案是:②④
【考点精析】掌握二次函数图象以及系数a、b、c的关系是解答本题的根本,需要知道二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
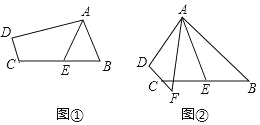
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试探究AB,AD,DC之间的等量关系,证明你的结论;
(2)如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,D在CB上,E为AB之中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE=( )
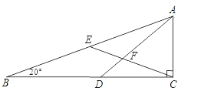
A. 40° B. 50° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户种植一种经济作物,总用水量y(m3)与种植时间x(天)之间的函数关系如图所示.
(1)第20天的总用水量为 m3;
(2)当x≥20时,求y与x之间的函数表达式;
(3)种植时间为多少天时,总用水量达到7 000 m3.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(3x2y)2(﹣15xy3)÷(﹣9x4y2)
(2)(2a﹣3)2﹣(1﹣a)2
(3)先化简,再求值:(2+x)(2﹣x)+(x﹣1)(x+5),其中x=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com