
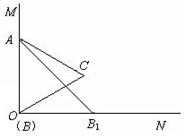
如图,已知∠MON=90º,等边△ABC的一个顶点A是射线OM上的一定点,顶点B与点O重合,顶点C在∠MON内部.
(1)当顶点B在射线ON上移动到B1时,连结AB1,请在∠MON内部作出以AB1为边的等边三角形AB1C1(保留作图痕迹,不写作法和证明);
(2)设AB1与OC交于点Q,AC的延长线与B1C1交于点D.求证:
![]()
(3)连结CC1,试猜想∠ACC1为多少度?并证明你的猜想.
 |
科目:初中数学 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
如图,已知∠MON=90°,等边三角形ABC的一个顶点A是射线OM上的一定点,顶点B与点O重合,顶点C在∠MON内部.
(1)当顶点B在射线ON上移动到B1时,连结AB1,请在∠MON内部作出以AB1为一边的等边三角形AB1C1(保留作图痕迹,不写作法和证明);
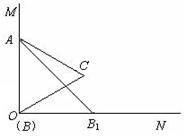
(2)设AB1与OC交于点Q,AC的延长线与B1C1交于点D.求证:△ACQ∽△AB1D;
(3)连结CC1,试猜想∠ACC1为多少度?并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
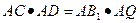
 |
查看答案和解析>>
科目:初中数学 来源:2011年潍城区教学质量检测九年级数学试题 题型:解答题
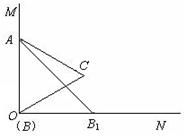
如图,已知∠MON=90º,等边△ABC的一个顶点A是射线OM上的一定点,顶点B与点O重合,顶点C在∠MON内部.
(1)当顶点B在射线ON上移动到B1时,连结AB1,请在∠MON内部作出以AB1为边的等边三角形AB1C1(保留作图痕迹,不写作法和证明);
(2)设AB1与OC交于点Q,AC的延长线与B1C1交于点D.求证: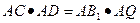
(3)连结CC1,试猜想∠ACC1为多少度?并证明你的猜想.
 |
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖北鄂州卷)数学 题型:解答题
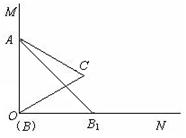
如图,已知∠MON=90º,等边△ABC的一个顶点A是射线OM上的一定点,顶点B与点O重合,顶点C在∠MON内部.
(1)当顶点B在射线ON上移动到B1时,连结AB1,请在∠MON内部作出以AB1为边的等边三角形AB1C1(保留作图痕迹,不写作法和证明);
(2)设AB1与OC交于点Q,AC的延长线与B1C1交于点D.求证:
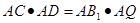
(3)连结CC1,试猜想∠ACC1为多少度?并证明你的猜想.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com