Question

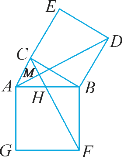
【题目】如图，在Rt△ABC中，∠ACB=90°，分别以AB、BC为一边向外作正方形ABFG、BCED，连接AD、CF，AD与CF交于点M，AB与CF交于点H.

（1）求证：△ABD≌△FBC；

（2）已知AD=6，求四边形AFDC的面积;

（3）在△ABC中，设BC=a，AC=b，AB=c，当∠ACB≠90°时，c≠a+b.在任意△ABC中，c=a+b+k.就a=3，b=2的情形，探究k的取值范围（只需写出你得到的结论即可）.

Answer 1

【答案】（1）详见解析；（2）18；（3）-12<k<12.

【解析】

（1）根据四边形ABFG、BCED是正方形得到两对边相等，一对直角相等，根据图形利用等式的性质得到一对角相等，利用SAS即可得到三角形全等；
（2）连接FD，由（1）的三角形全等，得到AD=FC，∠BAD=∠BFC，利用等式的性质及垂直定义得到AD与CF垂直，四边形AFDC面积=三角形ACD面积+三角形ACF面积+三角形DMF面积-三角形ACM面积，求出即可；
（3）根据a，b及c为三角形三边长，利用两边之和大于第三边，两边之差小于第三边列出关于c的不等式，将a与b的值代入求出c的范围，进而确定出c2的范围，即a2+b2+k的范围，即可求出k的范围．

（1）∵四边形ABFG、BCED是正方形，

∴AB=FB，CB=DB，∠ABF=∠CBD=90°，

∴∠ABF+∠ABC=∠CBD+∠ABC，

即∠ABD=∠CBF，

在△ABD和△FBC中，

，

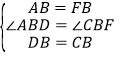∴△ABD≌△FBC（SAS）；

（2）连接FD，设CF与AB交于点N，

∵△ABD≌△FBC，

∴AD=FC，∠BAD=∠BFC，

∴∠AMF=180°﹣∠BAD﹣∠CNA=180°﹣（∠BFC+∠BNF）=180°﹣90°=90°，

∴AD⊥CF，

∵AD=6，

∴FC=AD=6，

∴S四边形AFDC=S△ACD+S△ACF+S△DMF﹣S△ACM，

=ADCM+CFAM+DMFM﹣AMCM，

=3CM+3AM+（6﹣AM）（6﹣CM）﹣AMCM，

=18；

（3）∵在△ABC中，设BC=a=3，AC=b=2，AB=c，

∴a﹣b＜c＜a+b，即1＜c＜5，

∴1＜c2＜25，即1＜a2+b2+k=13+k＜25，

解得：﹣12＜k＜12．