
分析 (1)先根据数的开方法则计算出各数,再去绝对值符号,根据实数的加减法则进行计算即可;
(2)先算乘方、开方,再算乘法,最后算加减即可;
(3)先把方程左边化为完全平方式的形式,再两边开平方即可得出结论.
(4)先把方程左边化为立方式的形式,再两边开立方即可得出结论.
解答 解:(1)原式=7-3-($\sqrt{2}$-1)
=4-$\sqrt{2}$+1
=5-$\sqrt{2}$;
(2)原式=2-2$\root{3}{2}$×$\frac{1}{4}$+$\sqrt{11}$-3
=$\sqrt{11}$-$\frac{\root{3}{2}}{2}$-1;
(3)方程两边同时除以2得,(x-1)2=4,
两边开方得,x-1=±2,
故x1=3,x2=-1;
(4)方程两边同时乘以8得,(2x+1)3=$\frac{8}{27}$,
两边开立方得,2x+1=$\frac{2}{3}$,即x=-$\frac{1}{6}$.
点评 本题考查的是实数的运算,熟知实数混合运算的法则及解一元二次方程的法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
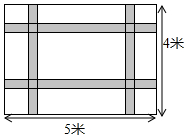 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.
如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
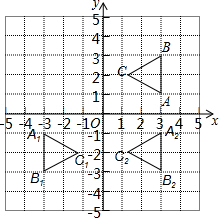 如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以原点为对称中心作△ABC的中心对称图形,得△A1B1C1,再以y轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以原点为对称中心作△ABC的中心对称图形,得△A1B1C1,再以y轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com