
����Ŀ����ͼ1����һ�����ǰ��ֱ���غϷ��ã����С�A��30�㣬��CDE��45�㣮
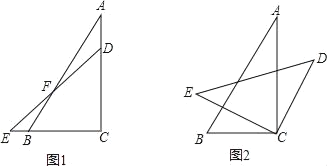
��1����ͼ1�����EFB�Ķ�����
��2�������ǰ�ACB��λ�ñ��ֲ����������ǰ�CDE����ֱ�Ƕ���C˳ʱ�뷽����ת��
�ٵ���ת����ͼ2��ʾλ��ʱ��ǡ��CD��AB�����ECB�Ķ���Ϊ�� ����
���������ǰ�CDE�����Ƶ�C��ת��ֱ���ص�ͼ1λ�ã�����һ�����У��Ƿ���ڡ�CDE����һ����ABƽ�У�������ڣ����㻭��ʾ��ͼ����ֱ��д����Ӧ�ġ�ECB�Ĵ�С����������ڣ���˵�����ɣ�
���𰸡���1����EFB��15�㣻��2����30�㣻�ڴ��ڣ�ͼ����������ECB��120�㡢165�㡢150�㡢60���15�㣮
��������
��1������ֱ���������ڽǺ͵����ʼ��ɵõ��𰸣�
��2���ٸ���ƽ���ߵ����ʼ��ɵõ��𰸣�
�ڷ�5��������ۣ�����ƽ���ߵ����ʽ��м��㣬���ɵõ���.
�⣺��1���ߡ�A��30������CDE��45����
���ABC��90����30����60������E��90����45����45����
���EFB����ABC����E��60����45����15����
��2���١�CD��AB��
���ACD����A��30����
�ߡ�ACD+��ACE����DCE��90����
��ECB+��ACE����ACB��90����
���ECB����ACD��30����
����ͼ1��CE��AB����ACE����A��30����
��ECB����ACB+��ACE��90��+30����120����
��ͼ2��DE��ABʱ���ӳ�CD��AB��F��
���BFC����D��45����
�ڡ�BCF�У���BCF��180������B����BFC��
��180����60����45����75����
����ECB����BCF+��ECF��75��+90����165����
��ͼ3��CD��ABʱ����BCD����B��60����
��ECB����BCD+��EDC��60��+90����150����
��ͼ4��CE��ABʱ����ECB����B��60����
��ͼ5��DE��ABʱ����ECB��60����45����15����




 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��C�ֱ���x�ᣬy���ϣ��ı���ABCOΪ���Σ�AB=16��AC=20,��D���A����y��Գƣ���E��F�ֱ����߶�AD��AC�ϵĶ��㣨��E�����A��D�غϣ����ҡ�CEF=��ACB.
��1��ֱ��д��BC�ij����� ������D���������� ����
��2��֤������AEF����DCE���ƣ�
��3������EFCΪ����������ʱ�����E��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס�����������ת����Ϸʱ������������������ת����ת��A��B��ÿ��ת�̱��ֳ������ȵļ������Σ�����ÿһ�������ڱ������֣���Ϸ����ͬʱת������ת�̣���ת��ֹͣ��ָ����ָ���������֮��Ϊ0ʱ����ʤ������֮��Ϊ1ʱ���һ�ʤ�����ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ��

��1���û���״ͼ���б������һ�ʤ�ĸ��ʣ�
��2�������Ϸ����Լס���˫����ƽ�����жϲ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O���Խ���ACΪ��O��ֱ��������C��AC�Ĵ��߽�AD���ӳ����ڵ�E����FΪCE���е㣬����DB��DC��DF��

��1�����CDE�Ķ�����
��2����֤��DF�ǡ�O�����ߣ�
��3����AC=2![]() DE����tan��ABD��ֵ��
DE����tan��ABD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ˮ���̳�ij��̨����ÿ̨���۷ֱ�Ϊ160Ԫ��120Ԫ��A��B�����ͺŵĵ���ȣ��±��ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 4̨ | 1200Ԫ |
�ڶ��� | 5̨ | 6̨ | 1900Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�����̳����ò�����7500Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�50̨����A���ͺŵĵ��������ܲɹ�����̨��
��3���ڣ�2���������£��̳���������50̨������ܷ�ʵ������1850Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD��AB=AC��E��F�ֱ���BC��AD���е㣬����AE��CF��
��1����֤���ı���AECF�Ǿ��Σ�
��2����AB=6������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���![]() ���������ϣ���B������Ϊ(3,4)һ�κ���
���������ϣ���B������Ϊ(3,4)һ�κ���![]() ��ͼ�����OC��AB�ֱ��ڵ�D��E����������OD= BE.��M���߶�DE�ϵ�һ������.
��ͼ�����OC��AB�ֱ��ڵ�D��E����������OD= BE.��M���߶�DE�ϵ�һ������.
(1)��b��ֵ��
(2)����OM����������ODM��������ı���OAEM�����֮��Ϊ1��3�����M�����ꣻ
(3)���N��![]() ���Ϸ�ƽ���ڵ�һ�㣬��O��D��M��NΪ������ı��������Σ����N������.
���Ϸ�ƽ���ڵ�һ�㣬��O��D��M��NΪ������ı��������Σ����N������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ���ϣ���ʦ������һ������
��֪����ͼ1����![]() �У�
�У�![]() ���ó߹���ͼ������
���ó߹���ͼ������![]() ��
��


ͬѧ�ǿ����Խ����˺ܶ�취������С������ͼ2������ͬѧ�Ƿ�����������
�ٷֱ��Ե�![]() ��
��![]() ΪԲ�ģ�����
ΪԲ�ģ�����![]() ��Ϊ�뾶�����������ֱ��ڵ�
��Ϊ�뾶�����������ֱ��ڵ�![]() ��
��![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��������![]() ����
����![]() ��ȡ��
��ȡ��![]() ��ʹ
��ʹ![]() ��
��
������![]() ��
��![]() ��
��
���ı���![]() �����������ľ��Σ�
�����������ľ��Σ�
��ʦ˵����С����������ȷ����
д��С������ͼ���ݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵����ۼס���������Ʒ������������Ϣ��

����������Ϣ������������⣺
��1����ס���������Ʒ�Ľ������ۣ�
��2����֪�ס���������Ʒ�����۵��۷ֱ�Ϊ2Ԫ��3Ԫ�����̵�ƽ��ÿ����������Ʒ500��������Ʒ1300�������г����鷢�֣�������Ʒ���۵���ÿ��0.1Ԫ��������Ʒÿ��ɶ�����100�����̵�����Ѽ�����Ʒ�����۵����½�m��m��0��Ԫ���ڲ������������ص������£���mΪ��ֵʱ���̵�ÿ�����ۼס���������Ʒ��ȡ��������Ϊ1800Ԫ��ע����������=���۵��۩��������ۣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com