
 如图,反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,过点A作AC⊥y轴与点C,过点B作BD⊥x轴于点D.
如图,反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,过点A作AC⊥y轴与点C,过点B作BD⊥x轴于点D.分析 (1)首先设A(x1,$\frac{k}{{x}_{1}}$),B(x2,$\frac{k}{{x}_{2}}$),可得AE=x1-x2,BE=$\frac{k}{{x}_{1}}$-$\frac{k}{{x}_{2}}$,EC=-x2,ED=$\frac{k}{{x}_{1}}$,即可求得$\frac{AE}{BE}=\frac{EC}{ED}$,继而证得结论.
(2)先求得直线与x轴、y轴的交点,然后根据AE∥OM,BE∥ON,∠E=∠MON=90°,求得△ABE∽△MNO,根据相似三角形的性质得出$\frac{AE}{BE}$=$\frac{OM}{ON}$=$\frac{1}{2}$,根据三角形的面积结合交点和系数的关系即可求得.
(3)延长AE到点F,使得EF=AE,连接BF,过点M作MG⊥BF于G,连接AM,如图2,则有EF=AE=3,∠MGB=∠FEB=90°,然后运用勾股定理可求出BF,易证△MGB∽△FEB,运用相似三角形的性质可得MG=$\frac{MB}{\sqrt{5}}$.从而得到T运动的时间为$\frac{MB}{\sqrt{5}}$+$\frac{MA}{1}$=MG+MA,根据两点之间线段最短可得:当A、M、G三点共线时,MG+MA最小,此时有∠AGB=90°,然后只需证到△AEM∽△BEF,运用相似三角形的性质求出EM,进而求出MD,就可得到点M的坐标.
解答 解:(1)设A(x1,$\frac{k}{{x}_{1}}$),B(x2,$\frac{k}{{x}_{2}}$),
根据题意AE=x1-x2,BE=$\frac{k}{{x}_{1}}$-$\frac{k}{{x}_{2}}$,EC=-x2,ED=$\frac{k}{{x}_{1}}$,
∵$\frac{AE}{BE}$=$\frac{{x}_{1}-{x}_{2}}{\frac{k}{{x}_{1}}-\frac{k}{{x}_{2}}}$=-$\frac{{x}_{1}{x}_{2}}{k}$,$\frac{EC}{ED}$=$\frac{-{x}_{2}}{\frac{k}{{x}_{1}}}$=-$\frac{{x}_{1}{x}_{2}}{k}$,
∴$\frac{AE}{BE}=\frac{EC}{ED}$,
∴$\frac{EC}{AE}$=$\frac{ED}{BE}$,
∴AB∥CD;
(2)∵a=2,
∴一次函数为y=2x-2,
∴直线y=2x-2交x轴M的坐标为(1,0),交y轴N的坐标为(0,-2),
∴OM=1,ON=2,
∵AC⊥y轴于点C,BD⊥x轴于点D.
∴AE∥OM,BE∥ON,∠E=∠MON=90°,
∴△ABE∽△MNO,
∴$\frac{AE}{BE}$=$\frac{OM}{ON}$=$\frac{1}{2}$,
∴BE=2AE,
∵AE=x1-x2,
∴BE=2(x1-x2),
由$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=2x-2}\end{array}\right.$,
得,x2-x-$\frac{k}{2}$=0,
∴x1+x2=1,x1x2=-$\frac{k}{2}$,
∵SABE=$\frac{1}{2}$AE•BE=$\frac{1}{2}$(x1-x2)•2(x1-x2)=(x1-x2)2=(x1+x2)2-4x1x2=1-4×(-$\frac{k}{2}$)=1+2k=9,
∴k=4,
∴反比例函数的解析式为y=$\frac{4}{x}$;
(3)∵反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,
∴$\left\{\begin{array}{l}{y=2x-2}\\{y=\frac{4}{x}}\end{array}\right.$,
解得:x1=2,x2=-1,
∴点A(2,2),(-1,-4),
∴E(-1,2),
∴BE=6,AE=3,
如图2,延长AE到点F,使得EF=AE,连接BF,过点M作MG⊥BF于G,连接AM,如图2,
则有EF=AE=3,∠MGB=∠FEB=90°.
∴BF=$\sqrt{E{F}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$.
∵∠GBM=∠EBF,∠MGB=∠FEB,
∴△MGB∽△FEB,
∴$\frac{MG}{MB}$=$\frac{FE}{FB}$=$\frac{3}{3\sqrt{5}}$,
∴MG=$\frac{MB}{\sqrt{5}}$.
由题可得:T运动的时间为$\frac{MB}{\sqrt{5}}$+$\frac{MA}{1}$=MG+MA,
根据两点之间线段最短可得:当A、M、G三点共线时,MG+MA最小,
此时AG⊥BF,即∠AGB=90°,
∴∠F+∠FAG=90°.
∵∠FEB=90°,
∴∠F+∠FBE=90°,
∴∠FAG=∠FBE.
又∵∠AEM=∠BEF=90°,
∴△AEM∽△BEF,
∴$\frac{EM}{EF}$=$\frac{AE}{BE}$,
∴$\frac{EM}{3}$=$\frac{3}{6}$,
∴EM=$\frac{3}{2}$,
∴MD=ED-EM=2-$\frac{3}{2}$=$\frac{1}{2}$,
∴点M的坐标为(-1,$\frac{1}{2}$).
点评 此题属于反比例函数综合题,考查了相似三角形的判定与性质、勾股定理、两点之间线段最短等知识.注意把T运动的时间$\frac{MB}{\sqrt{5}}$+$\frac{MA}{1}$转化为MG+MA是解决第(3)小题的关键,有一定的难度.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
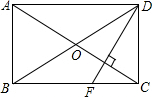 如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长10m、宽5m、深4m的长方体水池被隔成底面积分别是3m×5m和7m×5m的甲、乙两池(设隔墙厚度忽略不计),两池隔墙下方有阀门相连.
如图,长10m、宽5m、深4m的长方体水池被隔成底面积分别是3m×5m和7m×5m的甲、乙两池(设隔墙厚度忽略不计),两池隔墙下方有阀门相连.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物DE的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A处测得建筑物顶端D的仰角为53°,山坡AE的坡度i=1:5,潘老师在B处测得建筑物顶端D的仰角为45°.若此时刘老师与潘老师的距离AB=200m,求建筑物DE的高度.(sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,结果精确到0.1m)
重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物DE的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A处测得建筑物顶端D的仰角为53°,山坡AE的坡度i=1:5,潘老师在B处测得建筑物顶端D的仰角为45°.若此时刘老师与潘老师的距离AB=200m,求建筑物DE的高度.(sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com