Question

13．如图1，抛物线y=ax²+x+3（a≠0）与x轴的负半轴交于点A（-2，0），顶点为C，点B在抛物线上，且点B的横坐标为10，连接AB、BC、CA，BC与x轴交于点D．

（1）求点D的坐标；
（2）动点P在线段BC上，过点P作x轴的垂线，与抛物线交于点Q，过点Q作QH⊥BC于H，求△PQH的周长的最大值，并直接写出此时点H的坐标；
（3）如图2，以AC为对角线作正方形AMCN，将正方形AMCN在平面内平移得正方形A′M′C′N′，当正方形A′M′C′N′有顶点在△ABC的边AC上（不含端点）时，正方形A′M′C′N′与△ABC重叠部分得到的多边形能否为轴对称图形？如果能，求出此时重叠部分的面积S的值，或重叠部分面积S的取值范围；若不能，说明理由．

Answer 1

分析 （1）根据已知条件先求出点B、C，再求出直线BC即可得到点D坐标．
（2）过C作CE⊥AD垂足为E，如图1由△CDE∽△PQH得到QH：PH：PQ=DE：CE：CD=1：2：$\sqrt{5}$，求出PQ的最大值即可得到△PQH周长的最大值．
（3）①当A′在边AC上时（如图2）重叠得到的四边形或三角形不是轴对称图形．
②当点M′在AC上时（如图3）重叠部分不构成多边形．
③当C′在AC边上时，（ⅰ）点M′在△ABC外或AB边上，重叠得到的等腰直角三角形是轴对称图形（如图4）．点C′与点A重合时，s=0；点M′在AB边上时，s=4故0＜s≤4．（ⅱ）点M′在△ABC内，仅当AC′=C′M′时重叠部分的四边形是轴对称图形（如图5），可以得到s=16$\sqrt{2}$-16．
④当点N′在AC边上时，仅当C′在△ABC内或BC边上时，重叠部分得到的五边形是轴对称图形（如图6）得到s=8，当点C′在BC边上时（如图7），作CE⊥OD垂足为E，交C′N′于F，A′N′交AB于G，可以得到s=$\frac{136}{9}$．

解答 解：（1）∵抛物线y=ax²+x+3经过点A（-2，0），
∴4a-2+3=0，
∴a=-$\frac{1}{4}$，
∴抛物线解析式为y=-$\frac{1}{4}$x²+x+3，
∵y=-$\frac{1}{4}$x²+x+3=-$\frac{1}{4}$（x-2）²+4，
∴顶点C的坐标（2，4），
在y=-$\frac{1}{4}$x²+x+3中，∵x=10，y=-12，
∴点B坐标为（10，-12），
设直线BC解析式y+kx+b（k≠0），∵B、C在直线上，
∴$\left\{\begin{array}{l}{2k+b=4}\\{10k+b+-12}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$，
∴直线BC解析式为y=-2x+8，
在y=-2x+8中，当y=0时，x=4，
∴点D坐标为（4，0）．
（2）过C作CE⊥AD垂足为E，如图1，则E（2，0），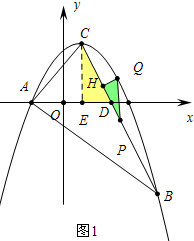

∴DE=2，CE=4，
∴CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=2$\sqrt{5}$，
∴DE：CE：CD=1：2：$\sqrt{5}$，
∵CE⊥x轴，PQ⊥x轴，
∴CE∥PQ，
∴∠ECD=∠QPE，
∵∠CED=∠QHP=90°，
∴△CDE∽△PQH，
∴QH：PH：PQ=DE：CE：CD=1：2：$\sqrt{5}$，
∴QH=$\frac{\sqrt{5}}{5}$PQ，PH=$\frac{2\sqrt{5}}{5}$PQ，
∴△PQH的周长=QH+PH+PQ=（1+$\frac{3\sqrt{5}}{5}$）PQ，
设P点坐标为（x，-2x+8），则点Q坐标（x，-$\frac{1}{4}$x²+x+3），
∴PQ=-$\frac{1}{4}$x²+x+3-（-2x+8）=-$\frac{1}{4}{x}^{2}$+3x-5=-$\frac{1}{4}$（x-6）²+4，
∴x=6时，PQ最大值=4，
∴△PQH周长最大值=4+$\frac{12\sqrt{5}}{5}$，
此时点H坐标（$\frac{22}{5}$，-$\frac{4}{5}$）．
（3）能，理由如下：
①当A′在边AC上时（如图2）重叠得到的四边形或三角形不是轴对称图形．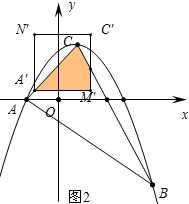

②当点M′在AC上时（如图3）重叠部分不构成多边形．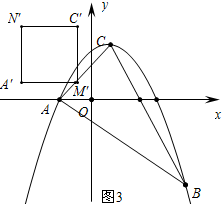

③当C′在AC边上时，
（ⅰ）点M′在△ABC外或AB边上，重叠得到的等腰直角三角形是轴对称图形（如图4）．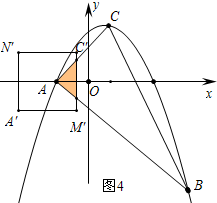

点C′与点A重合时，s=0；
点M′在AB边上时，
s=$\frac{1}{2}$C′M′•$\frac{1}{2}$C′M′=4，
∴0＜s≤4．
（ⅱ）点M′在△ABC内，仅当AC′=C′M′时重叠部分的四边形是轴对称图形（如图5）．

∵点A′必在CA的延长线上，
∴AA′=A′C′-AC′=4$\sqrt{2}-4$，
∴s=$\frac{1}{2}$A′M′²-$\frac{1}{2}$A′A²=16$\sqrt{2}$-16．
④当点N′在AC边上时，仅当C′在△ABC内或BC边上时，重叠部分得到的五边形是轴对称图形（如图6）．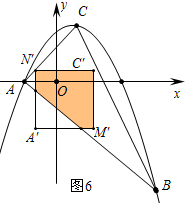

当点N′与A重合时，s=$\frac{1}{2}$A′M′²=8．
当点C′在BC边上时（如图7），作CE⊥OD垂足为E，交C′N′于F，A′N′交AB于G，
∵N′C′∥AD，
∴△CN′C′∽△CAD，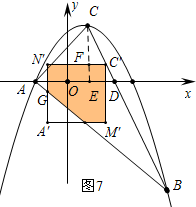

∴$\frac{CF}{CE}=\frac{N′C′}{AD}$，
∵CE=4，N′C′=4，AD=6，
∴CF=$\frac{8}{3}$，EF=CE-CF=$\frac{4}{3}$，GA′=N′A′-2EF=$\frac{4}{3}$，
∴s=A′N′²-$\frac{1}{2}$A′G²=$\frac{136}{9}$，
∴8＜s≤$\frac{136}{9}$，
综上所述，正方形A′M′C′N′与△ABC重叠部分得到的多边形能为轴对称图形，此时，0＜s≤4或s=16$\sqrt{2}$-16或8＜s≤$\frac{136}{9}$．

点评 本题考查二次函数、一次函数的图象与性质、正方形的性质、平移等知识，综合性比较强，有难度，学会分类讨论是解题的关键，解题中必须正确画出图形．