
【题目】如图,在半径为50的⊙O中,弦AB的长为50, 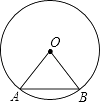
(1)求∠AOB的度数;
(2)求点O到AB的距离.
【答案】
(1)解:∵OA=OB=50,AB=50,
∴△OAB是等边三角形,
∴∠AOB=60°;
(2)解:过点O作OC⊥AB于点C,
则AC=BC= ![]() AB=25,
AB=25,
在Rt△OAC中,OC= ![]() =25
=25 ![]() .
.
即点O到AB的距离为25 ![]() .
.
【解析】(1)判断出三角形OAB是等边三角形即可得出∠AOB的度数;(2)过点O作OC⊥AB于点C,根据等边三角形的性质及勾股定理的知识,可求出OC.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于圆O,点E在对角线AC上. 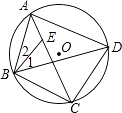
(1)若BC=DC,∠CBD=39°,求∠BCD的度数;
(2)若在AC上有一点E,且EC=BC=DC,求证:∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在RtABC中,∠ACB=90°,BAC=30°,BC=6. (I)如图①,将线段CA绕点C顺时针旋转30°,所得到与AB交于点M,则CM的长=;
(II)如图②,点D是边AC上一点D且AD=2 ![]() ,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 .
,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 . 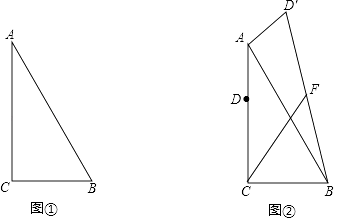
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
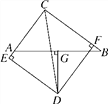
【题目】如图,在△ABC中,AC=6,BC=8,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
(1)求证:AE=BF;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费” 两部分组成.为了鼓励市民节约用水,其中城市供水费按阶梯式计费:一个月用水10吨以内(包括10吨)的用户,每吨收1.5元;一个月用水超过10吨的用户,10吨水仍按每吨1.5元收费,超过10吨的部分,按每吨2元收费.另外污水处理费按每吨0.65元收取.
(1)某居民5月份用水8吨,应交水费多少元? 6月份用水12吨,应交水费多少元?
(2)若某户某月用水x吨,请你用含有x的代数式表示该月应交的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图像如图所示,抛物线的对称轴为直线x=﹣1,P1(x1 , y1),P2(x2 , y2)是抛物线上的点,P3(x3 , y3)是直线l上的点,且x3<﹣1<x1<x2 , 则y1 , y2 , y3的大小关系是( ) 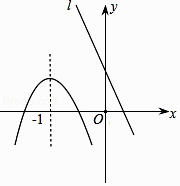
A.y1<y2<y3
B.y2<y3<y1
C.y3<y1<y2
D.y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点. (Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.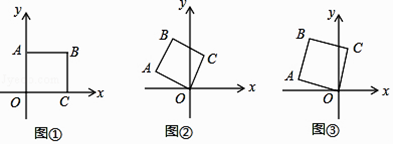
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com