
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:单选题
在平面直角坐标系中,点A(-1,3)与点B关于x轴对称,则点B的坐标是( )
A. (-1,-3) B. (-1,3) C. (1,3) D. (1,-3)
A 【解析】试题解析:∵点A(-1,3)关于x轴对称; ∴对称的点B的坐标是(-1,-3). 故选A.查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2017-2018学年度第一学期期末质量检测八年级数学试卷 题型:单选题
如图,A,B的坐标为(1,0),(0,2),若将线段AB平移至A1B1,则a﹣b的值为( )

A. 1 B. ﹣1 C. 0 D. 2
C 【解析】试题解析:由B点平移前后的纵坐标分别为2、4,可得B点向上平移了2个单位, 由A点平移前后的横坐标分别是为1、3,可得A点向右平移了2个单位, 由此得线段AB的平移的过程是:向上平移2个单位,再向右平移2个单位, 所以点A.B均按此规律平移, 由此可得a=0+2=2,b=0+2=2, ∴a?b=0, 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市、吴江、相城七年级第一学期期末数学统考试卷 题型:解答题
如图,延长线段AB到点C,使BC=3AB,点D是线段BC的中点,
(1)若设AB = x ,则BD = _________.
(2)若CD = 3cm ,求AC的长度.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市、吴江、相城七年级第一学期期末数学统考试卷 题型:填空题
已知 ,则
,则 的值是_________.
的值是_________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市、吴江、相城七年级第一学期期末数学统考试卷 题型:单选题
下列说法错误的是()
A. 两点之间线段最短 B. 过一点有且只有一条直线与已知直线垂直
C. 同角的余角相等 D. 过一点有且只有一条直线与已知直线平行
D 【解析】D说法错误,并不明确该点在直线上还是在直线外,当点在直线上时,过一点没有直线与已知直线平行;当点不在直线上时,过一点有且只有一条直线与已知直线平行. 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
(2015秋•浦口区校级期末)几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.
【回忆】
如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.

【探索】
(1)如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.

(2)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.

查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
若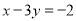 ,那么
,那么 的值是___________.
的值是___________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年八年级上学期期末数学试卷 题型:解答题
实验与操作:如图,  中,
中,  ,
,  是
是 的一个外角,根据要求进行尺规作图,并在图中表明相应的字母(保留作图痕迹,不写作法)
的一个外角,根据要求进行尺规作图,并在图中表明相应的字母(保留作图痕迹,不写作法)
( )作
)作 的平分线
的平分线 ,作线段
,作线段 的垂直平分线,与
的垂直平分线,与 交于点
交于点 ,与
,与 边交于点
边交于点 ,连结
,连结 .
.
(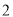 )猜测
)猜测 和
和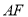 的数量关系,并说明理由.
的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com