

| 算式 | 与平方差公式a对应的项 | 与平方差公式中b对应的项 | 写成a2-b2的形式 | 计算结果 |
| (x+y)(x-y) | x | y | x2-y2 | x2-y2 |
| (m+3)(m-3) | m | 3 | m2-32 | m2-9 |
| (2x+1)(2x-1) | 2x | 1 | (2m)2-12 | 4m2-1 |
| (x+2y)(-x+2y) | x | 2y | x2-(2y)2 | x2-4y2 |
分析 (1)两个图形只是位置改变,因而面积相等;
(2)利用两种方法表示阴影部分是面积,据此即可证明公式.
解答 解:(1)两个图形(着色部分)的面积相等;
(2)第一个图形中阴影部分的面积是a2-b2,第二个图形的面积是(a+b)(a-b).
则(a+b)(a-b)=a2-b2.
| 算式 | 与平方差公式a对应的项 | 与平方差公式中b对应的项 | 写成a2-b2的形式 | 计算结果 |
| (x+y)(x-y) | x | y | x2-y2 | x2-y2 |
| (m+3)(m-3) | m | 3 | m2-32 | m2-9 |
| (2x+1)(2x-1) | 2x | 1 | (2m)2-12 | 4m2-1 |
| (x+2y)(-x+2y) | x | 2y | x2-(2y)2 | x2-4y2 |
点评 此题主要考查的是平方差公式的几何表示,运用不同方法表示阴影部分面积是解题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
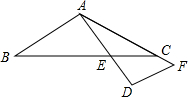 如图,在△ABC中,AB=AC,将AB边绕点A按逆时针方向旋转90°,得到线段AD,AD交BC边于点E,过点D作AD的垂线,交AC边的延长线于点F,若AE=9,DF=8,则线段DE的长为6.
如图,在△ABC中,AB=AC,将AB边绕点A按逆时针方向旋转90°,得到线段AD,AD交BC边于点E,过点D作AD的垂线,交AC边的延长线于点F,若AE=9,DF=8,则线段DE的长为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com