Question

7．如图，关于x的二次函数y=x²+bx+c与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为二次函数的顶点，已知点（-1，0），点C（0，-3），直线DE为二次函数的对称轴，交BC于点E，交x轴于点F．
（1）求抛物线的解析式和点D的坐标；
（2）直线DE上是否存在点M，使点M到x轴的距离于到BD的距离相等？若存在，求出点M的坐标；若不存在，请说明理由；
（3）已知点Q是线段BD上的动点，点D关于EQ的对称点是点D′，是否存在点Q使得△EQD′与△EQB的重叠部分图象为直角三角形？若存在，请求出DQ的长；若不存在，请说明理由．

Answer 1

分析 （1）根据待定系数法，求出抛物线解析式，再根据顶点坐标公式，即可求出顶点坐标；
（2）根据点M到x轴和BD的距离相等，即可得到点M在∠FBD的平分线上，根据全等即可求出BN的长度，从而求出DN的长度，根据勾股定理，列出方程，计算即可；
（3）分三种情况：①当点D′落在线段BD上，△EQD′与△EQB的重叠部分图象为直角三角形，故过点E作EQ⊥BD与点Q，根据相似三角形的性质即可求出DQ的长度；②当点D′落在线段BD的右侧时，△EQD′与△EQB的重叠部分图象为直角三角形，故过点E作ED′⊥BD，交BD于点M，且ED′=ED．根据锐角三角函数求出DQ的长度；③当点D′落在线段BD的左侧时，△EQD′与△EQB的重叠部分图象为直角三角形，故过点E作EM⊥BD于点M，作∠BEM的平分线EQ，交BD于点Q．

解答 解：（1）抛物线经过点A（-1，0），点C（0，-3），
可得：$\left\{\begin{array}{l}{1-b+c=0}\\{c=-3}\end{array}\right.$，解得：$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$，
∴抛物线解析式为：y=x²-2x-3，
∴$-\frac{b}{2a}=-\frac{-2}{2}=1$，$\frac{4ac-{b}^{2}}{4a}=\frac{-12-4}{4}=-4$，
∴顶点坐标D（1，-4）．
（2）存在．
①抛物线与x轴交于点B，可得点B（3，0），
过点M作MN⊥BD于点N，连接BE，如图1，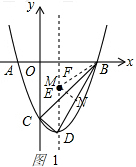
设点M的坐标为（1，-m），
∵MF=MN，MF⊥AB，MN⊥BD，
∴点M在∠FBD的平分线上，
∵BM=BM，
∴Rt△BFM≌Rt△BNM（HL），
∴BM=BF=2，
在Rt△BDF中，BF=2，DF=4，
∴BD=$\sqrt{{4}^{2}+{2}^{2}}=\sqrt{20}=2\sqrt{5}$，
∴DN=4-m，
在Rt△MND中，MN=m，DM=4-m，
∴${m}^{2}+（2\sqrt{5}-2）^{2}=（4-m）^{2}$，解得：m=$\sqrt{5}-1$，
∴点M（1，$1-\sqrt{5}$）．
（3）存在．
①设直线BC的解析式为y=kx+b，点B（3，0），点C（0，-3）在直线BC上，
∴$\left\{\begin{array}{l}{b=-3}\\{3k+b=0}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$，
∴直线BC的解析式为：y=x-3．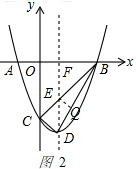
直线BC与直线DF相交于点E，可得点E（1，-2），
∴DE=-2-（-4）=2，
过点E作EQ⊥BD与点Q，此时点D′落在线段BD上，且△EQD′与△EQB的重叠部分图象为直角三角形，如图2，
由（2）可知，BD=$2\sqrt{5}$，
由△DEQ∽△DBF，得：$\frac{DQ}{DE}=\frac{DF}{DB}$，
即$\frac{DQ}{2}=\frac{4}{2\sqrt{5}}$，解得：DQ=$\frac{4\sqrt{5}}{5}$．
②过点E作ED′⊥BD，交BD于点M，且ED′=ED．
由点B（3，0），D（-1，4），可得y_BD=2x-6，
由ED′⊥BD，可得y_ED′=$-\frac{1}{2}x-\frac{3}{2}$，
联立$\left\{\begin{array}{l}{y=2x-6}\\{y=-\frac{1}{2}x-\frac{3}{2}}\end{array}\right.$，解得：$\left\{\begin{array}{l}{x=\frac{9}{5}}\\{y=-\frac{12}{5}}\end{array}\right.$，
∴点M（$\frac{9}{5}$，$-\frac{12}{5}$），
∴ED′=$\frac{2\sqrt{5}}{5}$，
由图2可知，DM=$\frac{4\sqrt{5}}{5}$，DE=2，
如图3，在Rt△EDM中，sin∠MED=$\frac{MD}{DE}$=$\frac{\frac{4\sqrt{5}}{5}}{2}=\frac{2\sqrt{5}}{5}$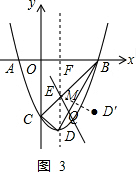
cos∠MED=$\frac{ME}{DE}=\frac{\frac{2\sqrt{5}}{5}}{2}=\frac{\sqrt{5}}{5}$，
∴tan∠QED′=$\frac{\frac{2\sqrt{5}}{5}}{1+\frac{\sqrt{5}}{5}}=\frac{\sqrt{5}-1}{2}$，
由点D与点D′关于EQ对称，可知，∠MEQ=$\frac{1}{2}$∠MED，
∴tan∠$\frac{QED′}{2}$=$\frac{MQ}{ME}=\frac{\sqrt{5}-1}{2}$，即$\frac{MQ}{\frac{2\sqrt{5}}{5}}=\frac{\sqrt{5}-1}{2}$，解得：MQ=1-$\frac{\sqrt{5}}{5}$，
∵BD=2$\sqrt{5}$，
∴DQ=MD-MQ=$\frac{4\sqrt{5}}{5}$-（1-$\frac{\sqrt{5}}{5}$）=$\sqrt{5}$-1．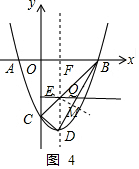
③过点E作EM⊥BD于点M，作∠BEM的平分线EQ，交BD于点Q，
∵点M（$\frac{9}{5}$，$-\frac{12}{5}$），点E（1，-2），点B（3，0），
由两点的距离公式，可得：EM=$\sqrt{（1-\frac{9}{5}）^{2}+（-2+\frac{12}{5}）^{2}}$=$\frac{2\sqrt{5}}{5}$，
BM=$\frac{6\sqrt{5}}{5}$，BE=2$\sqrt{2}$，
在Rt△BEM中，sin∠BEM=$\frac{BM}{BE}$=$\frac{3\sqrt{10}}{10}$，cos∠BEM=$\frac{EM}{BE}$=$\frac{\sqrt{10}}{10}$，
∴∠MEQ=$\frac{\frac{3\sqrt{10}}{10}}{1+\frac{\sqrt{10}}{10}}$=$\frac{\sqrt{10}-1}{3}$，
∴$\frac{MQ}{EM}=\frac{\sqrt{10}-1}{3}$，
即$\frac{MQ}{\frac{2\sqrt{5}}{5}}=\frac{\sqrt{10}-1}{3}$，解得：MQ=$\frac{10\sqrt{2}-2\sqrt{5}}{15}$，
∵DM=$\frac{4\sqrt{5}}{5}$，
∴DQ=DM+MQ=$\frac{10\sqrt{2}-2\sqrt{5}}{15}$+$\frac{4\sqrt{5}}{5}$=$\frac{2\sqrt{2}+2\sqrt{5}}{3}$．
综上所述，DQ的长度为：$\frac{4\sqrt{5}}{5}$或$\sqrt{5}$-1或$\frac{2\sqrt{2}+2\sqrt{5}}{3}$．

点评 本题主要考查二次函数与一次函数、相似三角形等知识的综合运用，能灵活应用各知识点是解决此题的关键．