练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．如图，在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃，设花圃的宽AB为x米，面积为y平方米．
    （1）求y与x之间的函数关系式；
    （2）当x取何值时所围成的花圃的面积最大？最大面积是多少？

    分析 （1）根据花圃的宽AB为x米，得出BC，再根据长方形的面积公式列式计算即可；
    （2）根据y与x之间的函数关系式求出函数的最值即可．

    解答 解：（1）∵花圃的宽AB为x米，
    ∴BC=（24-4x）米，
    ∴y=x（24-4x）=-4x2+24x；

    （2）∵y=-4x2+24x=-4（x-3）2+36，
    ∴当x=3时，y最大值=36，
    答；当x取3时所围成的花圃的面积最大，最大面积是36平方米．

    点评 本题主要考查了二次函数的应用，用到的知识点是二次函数的最值、二次函数的解析式、长方形的面积，能把实际问题转化成数学问题是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

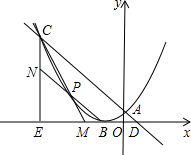    16．如图所示，已知点C（-3，m），点D（m-3，0）．直线CD交y轴于点A．作CE与X轴垂直，垂足为E，以点B（-1，0）为顶点的抛物线恰好经过点A、C．
    （1）则∠CDE=45°；
    （2）求抛物线对应的函数关系式；
    （3）设P（x，y）为抛物线上一点（其中-3＜x＜-1或-1＜x＜1，
    连结BP并延长交直线CE于点N，记N点的纵坐标为yN，连结CP并延长交X轴于点M．
    ①试证明：EM•（EC+yN）为定值；
    ②试判断EM+EC+yN是否有最小值，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．平面直角坐标系中，已知P1的坐标为（1，0），将其绕着原点按逆时针方向旋转30°得到点P2，延长OP2到P3，使OP3=2OP2，再将点P3绕着原点按逆时针方向旋转30°得到点P4，延长OP4到P5，使OP5=2OP4，如此继续下去，则点P2012的坐标是（${2}^{1006}\sqrt{3}$，-21005）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．按要求作图，并标出位置．
    （1）作出AB边上的高；
    （2）作出BC边上的中线；
    （3）作出∠ABC的角平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在图中求作一⊙P，使⊙P满足是以线段MN为弦且圆心P到∠AOB两边的距离相等，保留作图痕迹不写出作法．（要求：用尺规作图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，在Rt△ABC中，∠ABC=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为（　　）
    A．1B．1.5C．2D．2.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．在矩形纸片ABCD中，AB=6，BC=8．
    （1）将矩形纸片沿BD折叠，使点A落在点E处（如图①所示），连接DE，DE和BC相交于点F，试说明△BDF为等腰三角形，并求BF的长；
    （2）将矩形纸片折叠，使B与D重合（如图②所示），求折痕GH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

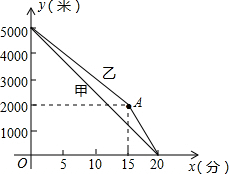    17．甲乙两名运动员进行长跑训练，两人距终点的路程y（米）与跑步时间x（分）之间的函数的图象如图所示，根据图象所提供的信息解答下列问题：
    （1）他们进行5000米的长跑训练，在0＜x＜15的时间段内，速度较快的人是甲；
    （2）求甲距终点的路程y（米）和跑步时间x（分）之间的函数关系式；
    （3）当x=15时，两人相距多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．某省去年底森林面积为2801700公顷，将2801700用科学记数法表示应为2.8017×106．

    查看答案和解析>>

    同步练习册答案