
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
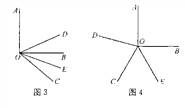
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

【答案】(1)45°;(2)45°;(3) ∠DOE的大小发生变化.45°或135°.
【解析】试题分析:
(1)因为∠DOE=∠COD+∠COE,所以分别根据角平分线的定义求出∠COD和∠COE即可;
(2)因为∠DOE=∠COD+∠COE,结合角平分线即可求解;
(3)需要分类,当∠AOC是钝角时和当∠AOC大于钝角时,结合角平分线求解.
试题解析:
(1) 根据题意得∠AOC=90°-∠BOC=20°.因为OD,OE分别平分∠AOC和∠BOC,所以∠COD=![]() ∠AOC=10°,∠COE=
∠AOC=10°,∠COE=![]() ∠BOC=35°,所以∠DOE=∠COD+∠COE=45°
∠BOC=35°,所以∠DOE=∠COD+∠COE=45°
(2) ∠DOE的大小不变,理由:∠DOE=∠COD+∠COE=![]() ∠AOC+
∠AOC+![]() ∠COB=
∠COB=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)= ![]() ∠AOB=45°
∠AOB=45°
(3) ∠DOE的大小发生变化.如图3,则∠DOE为45°;如图4,则∠DOE为135°


科目:初中数学 来源: 题型:
【题目】小方是一位密码编译爱好者,在他的密码手册中,有这样一条信息: ![]()
![]() ,分别对应下列六个字:州,爱,我,台,赞,美.现将
,分别对应下列六个字:州,爱,我,台,赞,美.现将 ![]() 因式分解,结果呈现的密码信息可能是( )
因式分解,结果呈现的密码信息可能是( )
A.赞美
B.台州赞
C.爱我台州
D.我爱美
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)在“十一”期间,小明等同学随家长共15人到游乐园游玩,成人门票每张50元,学生门票是6折优惠.他们购票共花了650元,求一共去了几个家长、几个学生?
(2)甲、乙两人骑自行车同时从相距65千米的两地出发相向而行,甲的速度是每小时17.5千米,乙的速度是每小时15千米,求经过几小时甲、乙两人相距32.5千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.
(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
摸到白球的频率 | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(1)按表格数据格式,表中的a=;b=;
(2)请估计:当次数s很大时,摸到白球的频率将会接近;
(3)请推算:摸到红球的概率是(精确到0.1);
(4)试估算:口袋中红球有多少只?
(5)解决了上面4个问题后,请你从统计与概率方面谈一条启示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①0是最小的整数; ②一个有理数,不是正数就是负数;
③a是正数,-a是负数; ④自然数一定是正数;
⑤非正数就是负数和0.
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】10月27日,巴中光雾山旅游景区迎来了今年红叶节开幕以来首个周末高峰,当日游客接待量达到5.1万次,其中5.1万精确到( )位。
A. 十分位B. 百位C. 千位D. 万位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图. 
(1)学校采用的调查方式是;学校共选取了名学生;
(2)补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他%;
(3)该校共有1100名学生,请估计喜欢“篮球”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com